butter (Signal Processing Toolbox)

Butterworth analog and digital filter design

Syntax

[b,a] = butter(n,Wn)
[b,a] = butter(n,Wn,'ftype')
[b,a] = butter(n,Wn,'s')
[b,a] = butter(n,Wn,'ftype','s')
[z,p,k] = butter(...)
[A,B,C,D] = butter(...)

Description

butter designs lowpass, bandpass, highpass, and bandstop digital and analog Butterworth filters. Butterworth filters are characterized by a magnitude response that is maximally flat in the passband and monotonic overall.

Butterworth filters sacrifice rolloff steepness for monotonicity in the pass- and stopbands. Unless the smoothness of the Butterworth filter is needed, an elliptic or Chebyshev filter can generally provide steeper rolloff characteristics with a lower filter order.

Digital Domain

[b,a] = butter(n,Wn) designs an order n lowpass digital Butterworth filter with normalized cutoff frequency Wn. It returns the filter coefficients in length n+1 row vectors b and a, with coefficients in descending powers of z.

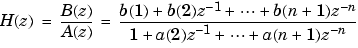
Cutoff frequency is that frequency where the magnitude response of the filter is 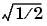. For butter, the normalized cutoff frequency Wn must be a number between 0 and 1, where 1 corresponds to the Nyquist frequency, 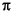radians per sample.

If Wn is a two-element vector, Wn = [w1 w2], butter returns an order 2*n digital bandpass filter with passband w1 < < w2.

[b,a] = butter(n,Wn,'ftype') designs a highpass, lowpass, or bandstop filter, where the string 'ftype' is one of the following.

'high' for a highpass digital filter with normalized cutoff frequency Wn
'low' for a lowpass digital filter with normalized cutoff frequency Wn
'stop' for an order 2*n bandstop digital filter if Wn is a two-element vector, Wn = [w1 w2]. The stopband is w1 < < w2.

With different numbers of output arguments, butter directly obtains other realizations of the filter. To obtain zero-pole-gain form, use three output arguments as shown below:

[z,p,k] = butter(n,Wn) or

[z,p,k] = butter(n,Wn,'ftype') returns the zeros and poles in length n column vectors z and p, and the gain in the scalar k.

To obtain state-space form, use four output arguments as shown below:

[A,B,C,D] = butter(n,Wn) or

[A,B,C,D] = butter(n,Wn,'ftype') where A, B, C, and D are

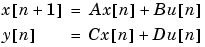
and u is the input, x is the state vector, and y is the output.

Analog Domain

[b,a] = butter(n,Wn,'s') designs an order n lowpass analog Butterworth filter with angular cutoff frequency Wn rad/s. It returns the filter coefficients in the length n+1 row vectors b and a, in descending powers of s, derived from this transfer function:

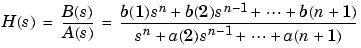
butter's angular cutoff frequency Wn must be greater than 0 rad/s.

If Wn is a two-element vector with w1 < w2, butter(n,Wn,'s') returns an order 2*n bandpass analog filter with passband w1 < < w2.

[b,a] = butter(n,Wn,'ftype','s') designs a highpass, lowpass, or bandstop filter.

With different numbers of output arguments, butter directly obtains other realizations of the analog filter. To obtain zero-pole-gain form, use three output arguments as shown below:

[z,p,k] = butter(n,Wn,'s') or

[z,p,k] = butter(n,Wn,'ftype','s') returns the zeros and poles in length n or 2*n column vectors z and p and the gain in the scalar k.

To obtain state-space form, use four output arguments as shown below:

[A,B,C,D] = butter(n,Wn,'s') or

[A,B,C,D] = butter(n,Wn,'ftype','s') where A, B, C, and D are

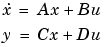
and u is the input, x is the state vector, and y is the output.

Examples

Example 1

For data sampled at 1000 Hz, design a 9th-order highpass Butterworth filter with cutoff frequency of 300 Hz, which corresponds to a normalized value of 0.6:

```
[b,a] = butter(9,300/500,'high');
```

The filter's frequency response is

```
freqz(b,a,128,1000)
```

Example 2

Design a 10th-order bandpass Butterworth filter with a passband from 100 to 200 Hz and plot its impulse response, or unit sample response:

n = 5; Wn = [100 200]/500;
[b,a] = butter(n,Wn);
[y,t] = impz(b,a,101);
stem(t,y)

Limitations

For high order filters, the state-space form is the most numerically accurate, followed by the zero-pole-gain form. The transfer function coefficient form is the least accurate; numerical problems can arise for filter orders as low as 15.

Algorithm

butter uses a five-step algorithm:

It finds the lowpass analog prototype poles, zeros, and gain using the buttap function.
It converts the poles, zeros, and gain into state-space form.
It transforms the lowpass filter into a bandpass, highpass, or bandstop filter with desired cutoff frequencies, using a state-space transformation.
For digital filter design, butter uses bilinear to convert the analog filter into a digital filter through a bilinear transformation with frequency prewarping. Careful frequency adjustment guarantees that the analog filters and the digital filters will have the same frequency response magnitude at Wn or w1 and w2.
It converts the state-space filter back to transfer function or zero-pole-gain form, as required.

See Also

besself, buttap, buttord, cheby1, cheby2, ellip, maxflat

buttap buttord