| Signal Processing Toolbox | |
Filter Discretization
The third step in the analog prototyping technique is the transformation of the filter to the discrete-time domain. The toolbox provides two methods for this: the impulse invariant and bilinear transformations. The filter design functions butter, cheby1, cheby2, and ellip use the bilinear transformation for discretization in this step.
| Analog to Digital Transformation |
Transformation Function |
| Impulse invariance |
[numd,dend] |
| Bilinear transform |
[zd,pd,kd][numd,dend][Ad,Bd,Cd,Dd] |
Impulse Invariance
The toolbox function impinvar creates a digital filter whose impulse response is the samples of the continuous impulse response of an analog filter. This function works only on filters in transfer function form. For best results, the analog filter should have negligible frequency content above half the sampling frequency, because such high frequency content is aliased into lower bands upon sampling. Impulse invariance works for some lowpass and bandpass filters, but is not appropriate for highpass and bandstop filters.
Design a Chebyshev Type I filter and plot its frequency and phase response using FVTool:
Click on the Magnitude and Phase Response toolbar button.
Impulse invariance retains the cutoff frequencies of 0.1 Hz and 0.5 Hz.
Bilinear Transformation
The bilinear transformation is a nonlinear mapping of the continuous domain to the discrete domain; it maps the s-plane into the z-plane by
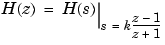
Bilinear transformation maps the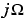 
-axis of the continuous domain to the unit circle of the discrete domain according to
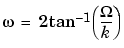
The toolbox function bilinear implements this operation, where the frequency warping constant k is equal to twice the sampling frequency (2*fs) by default, and equal to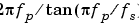 
if you give bilinear a trailing argument that represents a "match" frequency Fp. If a match frequency Fp (in hertz) is present, bilinear maps the frequency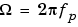 
(in rad/s) to the same frequency in the discrete domain, normalized to the sampling rate: 
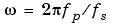(in rad/sample).
The bilinear function can perform this transformation on three different linear system representations: zero-pole-gain, transfer function, and state-space form. Try calling bilinear with the state-space matrices that describe the Chebyshev Type I filter from the previous section, using a sampling frequency of 2 Hz, and retaining the lower band edge of 0.1 Hz:
The frequency response of the resulting digital filter is
Click on the Magnitude and Phase Response toolbar button.
The lower band edge is at 0.1 Hz as expected. Notice, however, that the upper band edge is slightly less than 0.5 Hz, although in the analog domain it was exactly 0.5 Hz. This illustrates the nonlinear nature of the bilinear transformation. To counteract this nonlinearity, it is necessary to create analog domain filters with "prewarped" band edges, which map to the correct locations upon bilinear transformation. Here the prewarped frequencies u1 and u2 generate Bw and Wo for the lp2bp function:
fs = 2; % Sampling frequency (hertz) u1 = 2*fs*tan(0.1*(2*pi/fs)/2); % Lower band edge (rad/s) u2 = 2*fs*tan(0.5*(2*pi/fs)/2); % Upper band edge (rad/s) Bw = u2 - u1; % Bandwidth Wo = sqrt(u1*u2); % Center frequency [At,Bt,Ct,Dt] = lp2bp(A,B,C,D,Wo,Bw);
A digital bandpass filter with correct band edges 0.1 and 0.5 times the Nyquist frequency is
The example bandpass filters from the last two sections could also be created in one statement using the complete IIR design function cheby1. For instance, an analog version of the example Chebyshev filter is
Note that the band edges are in rad/s for analog filters, whereas for the digital case, frequency is normalized:
All of the complete design functions call bilinear internally. They prewarp the band edges as needed to obtain the correct digital filter.
| | Frequency Transformation | Filter Implementation | |
© 1994-2005 The MathWorks, Inc.
