

| Signal Processing Toolbox |   |
Constrained least square, lowpass and highpass, linear phase, FIR filter design
Syntax
b=fircls1(n,wo,dp,ds) b=fircls1(n,wo,dp,ds,'high') b=fircls1(n,wo,dp,ds,wt) b=fircls1(n,wo,dp,ds,wt,'high') b=fircls1(n,wo,dp,ds,wp,ws,k) b=fircls1(n,wo,dp,ds,wp,ws,k,'high') b=fircls1(n,wo,dp,ds,...,'design_flag')
Description
b generates a lowpass FIR filter = fircls1(n,wo,dp,ds)
b, where n+1 is the filter length, wo is the normalized cutoff frequency in the range between 0 and 1 (where 1 corresponds to the Nyquist frequency), dp is the maximum passband deviation from 1 (passband ripple), and ds is the maximum stopband deviation from 0 (stopband ripple).
b generates a highpass FIR filter = fircls1(n,wo,dp,ds,'high')
b. fircls1 always uses an even filter order for the highpass configuration. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, fircls1 increments it by 1.
b and = fircls1(n,wo,dp,ds,wt)
b specifies a frequency = fircls1(n,wo,dp,ds,wt,'high')
wt above which (for wt > wo) or below which (for wt < wo) the filter is guaranteed to meet the given band criterion. This will help you design a filter that meets a passband or stopband edge requirement. There are four cases:
0 < wt < wo < 1: the amplitude of the filter is within dp of 1 over the frequency range 0 <  <
< wt.
0 < wo < wt < 1: the amplitude of the filter is within ds of 0 over the frequency range wt <  <
< 1.
b generates a lowpass FIR filter = fircls1(n,wo,dp,ds,wp,ws,k)
b with a weighted function, where n+1 is the filter length, wo is the normalized cutoff frequency, dp is the maximum passband deviation from 1 (passband ripple), and ds is the maximum stopband deviation from 0 (stopband ripple). wp is the passband edge of the L2 weight function and ws is the stopband edge of the L2 weight function, where wp < wo < ws. k is the ratio (passband L2 error)/(stopband L2 error)
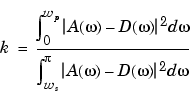
b generates a highpass FIR filter = fircls1(n,wo,dp,ds,wp,ws,k,'high')
b with a weighted function, where ws < wo < wp.
b enables you to monitor the filter design, where = fircls1(n,wo,dp,ds,...,'design_flag')
'design_flag' can be
'trace', for a textual display of the design table used in the design
'plots', for plots of the filter's magnitude, group delay, and zeros and poles. All plots are updated at each iteration step. The O's on the plot are the estimated extremals of the new iteration and the X's are the estimated extremals of the previous iteration, where the extremals are the peaks (maximum and minimum) of the filter ripples. Only ripples that have a corresponding O and X are made equal.
'both', for both the textual display and plots
Note
In the design of very narrow band filters with small dp and ds, there may not exist a filter of the given length that meets the specifications. |
Examples
Design an order 55 lowpass filter with a cutoff frequency at 0.3:
n = 55; wo = 0.3; dp = 0.02; ds = 0.008; b = fircls1(n,wo,dp,ds,'both'); % Display plots of the bands Bound Violation = 0.0870385343920 Bound Violation = 0.0149343456540 Bound Violation = 0.0056513587932 Bound Violation = 0.0001056264205 Bound Violation = 0.0000967624352 Bound Violation = 0.0000000226538 Bound Violation = 0.0000000000038 % The above Bound Violations indicate iterations as % the design converges. fvtool(b) % Display magnitude plot
Algorithm
fircls1 uses an iterative least-squares algorithm to obtain an equiripple response. The algorithm is a multiple exchange algorithm that uses Lagrange multipliers and Kuhn-Tucker conditions on each iteration.
See Also
References
[1] Selesnick, I.W., M. Lang, and C.S. Burrus, "Constrained Least Square Design of FIR Filters without Specified Transition Bands," Proceedings of the IEEE Int. Conf. Acoust., Speech, Signal Processing, Vol. 2 (May 1995), pp. 1260-1263.
[2] Selesnick, I.W., M. Lang, and C.S. Burrus, "Constrained Least Square Design of FIR Filters without Specified Transition Bands," IEEE Transactions on Signal Processing, Vol. 44, No. 8 (August 1996).
 | fircls | firls |  |
© 1994-2005 The MathWorks, Inc.