

| Signal Processing Toolbox |   |
Parks-McClellan optimal FIR filter design
Syntax
b=firpm(n,f,a) b=firpm(n,f,a,w) b=firpm(n,f,a,'ftype') b=firpm(n,f,a,w,'ftype') b=firpm(...,{lgrid}) [b,err]=firpm(...) [b,err,res]=firpm(...) b=firpm(n,f,@fresp,w) b=firpm(n,f,@fresp,w,'ftype')
Description
firpm designs a linear-phase FIR filter using the Parks-McClellan algorithm [1]. The Parks-McClellan algorithm uses the firpm exchange algorithm and Chebyshev approximation theory to design filters with an optimal fit between the desired and actual frequency responses. The filters are optimal in the sense that the maximum error between the desired frequency response and the actual frequency response is minimized. Filters designed this way exhibit an equiripple behavior in their frequency responses and are sometimes called equiripple filters. firpm exhibits discontinuities at the head and tail of its impulse response due to this equiripple nature.
b returns row vector = firpm(n,f,a)
b containing the n+1 coefficients of the order n FIR filter whose frequency-amplitude characteristics match those given by vectors f and a.
The output filter coefficients (taps) in b obey the symmetry relation:
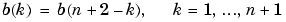
Vectors f and a specify the frequency-magnitude characteristics of the filter:
f is a vector of pairs of normalized frequency points, specified in the range between 0 and 1, where 1 corresponds to the Nyquist frequency. The frequencies must be in increasing order.
a is a vector containing the desired amplitudes at the points specified in f.
The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k odd is the line segment connecting the points (f(k), a(k)) and (f(k+1), a(k+1)).
The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k even is unspecified. The areas between such points are transition or "don't care" regions.
The relationship between the f and a vectors in defining a desired frequency response is shown in the illustration below.
firpm always uses an even filter order for configurations with a passband at the Nyquist frequency. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, firpm increments it by 1.
b = firpm(n,f,a,w)
uses the weights in vector w to weight the fit in each frequency band. The length of w is half the length of f and a, so there is exactly one weight per band.
b specify a filter type, where = firpm(n,f,a,w,'ftype')
'ftype' is
The output coefficients in b obey the relation b(k) = -b(n+2-k), k = 1, ..., n + 1. This class of filters includes the Hilbert transformer, which has a desired amplitude of 1 across the entire band.
designs an approximate FIR Hilbert transformer of length 31.
For nonzero amplitude bands, it weights the error by a factor of 1/f so that the error at low frequencies is much smaller than at high frequencies. For FIR differentiators, which have an amplitude characteristic proportional to frequency, these filters minimize the maximum relative error (the maximum of the ratio of the error to the desired amplitude).
b = firpm(...,{lgrid})
lgrid to control the density of the frequency grid, which has roughly (lgrid*n)/(2*bw) frequency points, where bw is the fraction of the total frequency band interval [0,1] covered by f. Increasing lgrid often results in filters that more exactly match an equiripple filter, but that take longer to compute. The default value of 16 is the minimum value that should be specified for lgrid. Note that the {lgrid} argument must be a 1-by-1 cell array.
[b,err] returns the maximum ripple height in err. = firpm(...)
[b,err,res] = firpm(...)
res with the following fields.
You can also use firpm to write a function that defines the desired frequency response. The predefined frequency response function handle for firpm is @firpmfrf, which designs a linear-phase FIR filter.
b returns row vector = firpm(n,f,@fresp,w)
b containing the n+1 coefficients of the order n FIR filter whose frequency-amplitude characteristics best approximate the response returned by function handle @fresp. The function is called from within firpm with the following syntax.
The arguments are similar to those for firpm:
n is the filter order.
f is the vector of normalized frequency band edges that appear monotonically between 0 and 1, where 1 is the Nyquist frequency.
gf is a vector of grid points that have been linearly interpolated over each specified frequency band by firpm. gf determines the frequency grid at which the response function must be evaluated, and contains the same data returned by cfirpm in the fgrid field of the opt structure.
w is a vector of real, positive weights, one per band, used during optimization. w is optional in the call to firpm; if not specified, it is set to unity weighting before being passed to fresp.
dh and dw are the desired complex frequency response and band weight vectors, respectively, evaluated at each frequency in grid gf.
b designs antisymmetric (odd) filters, where = firpm(n,f,@fresp,w,'ftype')
'ftype' is either 'd' for a differentiator or 'h' for a Hilbert transformer. If you do not specify an ftype, a call is made to fresp to determine the default symmetry property sym. This call is made using the syntax.
The arguments n, f, w, etc., may be used as necessary in determining an appropriate value for sym, which firpm expects to be either 'even' or 'odd'. If fresp does not support this calling syntax, firpm defaults to even symmetry.
Examples
Graph the desired and actual frequency responses of a 17th-order Parks-McClellan bandpass filter:
f=[0 0.3 0.4 0.6 0.7 1]; a=[0 0 1 1 0 0]; b=firpm(17,f,a); [h,w]=freqz(b,1,512); plot(f,a,w/pi,abs(h)) legend('Ideal','firpm Design')
Algorithm
firpm is a MEX-file version of the original Fortran code from [1], altered to design arbitrarily long filters with arbitrarily many linear bands.
firpm designs type I, II, III, and IV linear-phase filters. Type I and type II are the defaults for n even and n odd, respectively, while type III (n even) and type IV (n odd) are obtained with the 'hilbert' and 'differentiator' flags. The different types of filters have different symmetries and certain constraints on their frequency responses (see [5] for more details).
Diagnostics
If you get the following warning message,
it is possible that the filter design may still be correct. Verify the design by checking its frequency response.
See Also
butter, cheby1, cheby2, cfirpm, ellip, fir1, fir2, fircls, fircls1, firls, firrcos, firgr, firpmord, function_handle, yulewalk
References
[1] Programs for Digital Signal Processing, IEEE Press, New York, 1979, Algorithm 5.1.
[2] Selected Papers in Digital Signal Processing, II, IEEE Press, New York, 1979.
[3] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, New York:, 1987, p. 83.
[4] Rabiner, L.R., J.H. McClellan, and T.W. Parks, "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximations," Proc. IEEE 63 (1975).
[5] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1989, pp. 256-266.
 | firls | firpmord |  |
© 1994-2005 The MathWorks, Inc.