

| Signal Processing Toolbox |   |
Least square linear-phase FIR filter design
Syntax
Description
firls designs a linear-phase FIR filter that minimizes the weighted, integrated squared error between an ideal piecewise linear function and the magnitude response of the filter over a set of desired frequency bands.
b returns row vector = firls(n,f,a)
b containing the n+1 coefficients of the order n FIR filter whose frequency-amplitude characteristics approximately match those given by vectors f and a. The output filter coefficients, or "taps," in b obey the symmetry relation.
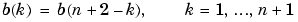
These are type I (n odd) and type II (n even) linear-phase filters. Vectors f and a specify the frequency-amplitude characteristics of the filter:
f is a vector of pairs of frequency points, specified in the range between 0 and 1, where 1 corresponds to the Nyquist frequency. The frequencies must be in increasing order. Duplicate frequency points are allowed and, in fact, can be used to design a filter exactly the same as those returned by the fir1 and fir2 functions with a rectangular (rectwin) window.
a is a vector containing the desired amplitude at the points specified in f.
The desired amplitude function at frequencies between pairs of points (f(k), f(k+1)) for k odd is the line segment connecting the points (f(k), a(k)) and (f(k+1), a(k+1)).
The desired amplitude function at frequencies between pairs of points (f(k), f(k+1)) for k even is unspecified. These are transition or "don't care" regions.
firls always uses an even filter order for configurations with a passband at the Nyquist frequency. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, firls increments it by 1.
The figure below illustrates the relationship between the f and a vectors in defining a desired amplitude response.
The f vector is 0, .3, .4, .6, .7, and .9 and is plotted on the x-axis. The a vector is 0, 1, 0, 0, .5, and .5 and is plotted on the y-axis. For normalized frequency from 0 to 0.3, the desired amplitude rises linearly from 0 to 1.0. A don't care region occurs from frequency 0.3 to 0.4. From frequency 0.4 to 0.6, the amplitude is zero. Another don't care region occurs from frequency 0.6 to 0.7. From frequency 0.7 to 0.9, the amplitude is 0.5. A final don't care region occurs from frequency 0.9 to 1.0 (Nyquist).
b uses the weights in vector = firls(n,f,a,w)
w to weight the fit in each frequency band. The length of w is half the length of f and a, so there is exactly one weight per band.
b specify a filter type, where = firls(n,f,a,w,'ftype')
'ftype' is:
'hilbert' for linear-phase filters with odd symmetry (type III and type IV). The output coefficients in b obey the relation b(k) = -b(n+2-k), k = 1, ... , n + 1. This class of filters includes the Hilbert transformer, which has a desired amplitude of 1 across the entire band.
'differentiator' for type III and type IV filters, using a special weighting technique. For nonzero amplitude bands, the integrated squared error has a weight of (1/f)2 so that the error at low frequencies is much smaller than at high frequencies. For FIR differentiators, which have an amplitude characteristic proportional to frequency, the filters minimize the relative integrated squared error (the integral of the square of the ratio of the error to the desired amplitude).
Example 1
Design an order 255 lowpass filter with transition band:
Example 2
Design a 31 coefficient differentiator:
An ideal differentiator has the response D(w) = jw. The amplitudes include a pi multiplier because the frequencies are normalized by pi.
Example 3
Design a 24th-order anti-symmetric filter with piecewise linear passbands and plot the desired and actual frequency response:
F=[0 0.3 0.4 0.6 0.7 0.9]; A=[0 1 0 0 0.5 0.5]; b=firls(24,F,A,'hilbert'); for i=1:2:6, plot([F(i) F(i+1)],[A(i) A(i+1)],'--'), hold on end [H,f]=freqz(b,1,512,2); plot(f,abs(H)), grid on, hold off legend('Ideal','firls Design')
Algorithm
Reference [1] describes the theoretical approach behind firls. The function solves a system of linear equations involving an inner product matrix of size roughly n/2 using the MATLAB \ operator.
This function designs type I, II, III, and IV linear-phase filters. Type I and II are the defaults for n even and odd respectively, while the 'hilbert' and 'differentiator' flags produce type III (n even) and IV (n odd) filters. The various filter types have different symmetries and constraints on their frequency responses (see [2] for details).
Diagnostics
One of the following diagnostic messages is displayed when an incorrect argument is used:
F must be even length. F and A must be equal lengths. Requires symmetry to be 'hilbert' or 'differentiator'. Requires one weight per band. Frequencies in F must be nondecreasing. Frequencies in F must be in range [0,1].
A more serious warning message is
This tends to happen when the product of the filter length and transition width grows large. In this case, the filter coefficients b might not represent the desired filter. You can check the filter by looking at its frequency response.
See Also
References
[1] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, 1987, pp. 54-83.
[2] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, 1989, pp. 256-266.
 | fircls1 | firpm |  |
© 1994-2005 The MathWorks, Inc.