maxflat (Signal Processing Toolbox)

Generalized digital Butterworth filter design

Syntax

[b,a] = maxflat(n,m,Wn)
b = maxflat(n,'sym',Wn)
[b,a,b1,b2] = maxflat(n,m,Wn)
[b,a,b1,b2,sos,g] = maxflat(n,m,Wn)
[...] = maxflat(n,m,Wn,'design_flag')

Description

[b,a] = maxflat(n,m,Wn) is a lowpass Butterworth filter with numerator and denominator coefficients b and a of orders n and m respectively. Wn is the normalized cutoff frequency at which the magnitude response of the filter is equal to 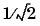(approx. -3 dB). Wn must be between 0 and 1, where 1 corresponds to the Nyquist frequency.

b = maxflat(n,'sym',Wn) is a symmetric FIR Butterworth filter. n must be even, and Wn is restricted to a subinterval of [0,1]. The function raises an error if Wn is specified outside of this subinterval.

[b,a,b1,b2] = maxflat(n,m,Wn) returns two polynomials b1 and b2 whose product is equal to the numerator polynomial b (that is, b = conv(b1,b2)). b1 contains all the zeros at z = -1, and b2 contains all the other zeros.

[b,a,b1,b2,sos,g] = maxflat(n,m,Wn) returns the second-order sections representation of the filter as the filter matrix sos and the gain g.

[...] = maxflat(n,m,Wn,'design_flag') enables you to monitor the filter design, where 'design_flag' is

'trace' for a textual display of the design table used in the design
'plots' for plots of the filter's magnitude, group delay, and zeros and poles
'both' for both the textual display and plots

Examples

n = 10; m = 2; Wn = 0.2;
[b,a] = maxflat(n,m,Wn)
fvtool(b,a)                       % Display the magnitude plot

Algorithm

The method consists of the use of formulae, polynomial root finding, and a transformation of polynomial roots.

See Also

butter, filter, freqz

References

[1] Selesnick, I.W., and C.S. Burrus, "Generalized Digital Butterworth Filter Design," Proceedings of the IEEE Int. Conf. Acoust., Speech, Signal Processing, Vol. 3 (May 1996).

lsf2poly medfilt1