mscohere (Signal Processing Toolbox)

Magnitude squared coherence function

Syntax

Cxy = mscohere(x,y)
Cxy = mscohere(x,y,window)
Cxy = mscohere(x,y,window,noverlap)
[Cxy,W] = mscohere(x,y,window,noverlap,nfft)
[Cxy,F] = mscohere(x,y,window,noverlap,nfft,fs)
[...] = mscohere(x,y,...,'whole')
mscohere(x,y,...)

Description

Cxy = mscohere(x,y) finds the magnitude squared coherence estimate Cxy of the input signals x and y using Welch's averaged, modified periodogram method. The magnitude squared coherence estimate is a function of frequency with values between 0 and 1 that indicates how well x corresponds to y at each frequency. The coherence is a function of the power spectral density (Pxx and Pyy) of x and y and the cross power spectral density (Pxy) of x and y.

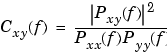
x and y must be the same length. For real x and y, mscohere returns a one-sided coherence estimate and for complex x or y, it returns a two-sided estimate.

mscohere uses the following default values:

Parameter
Description
Default Value

nfft
FFT length which determines the frequencies at which the coherence is estimated

For real x and y, the length of Cxy is (nfft/2+1) if nfft is even or (nfft+1)/2 if nfft is odd. For complex x or y, the length of Cxy is nfft.

If nfft is greater than the signal length, the data is zero-padded. If nfft is less than the signal length, the segment is wrapped using datawrap so that the length is equal to nfft.
Maximum of 256 or the next power of 2 greater than the length of each section of x or y

fs
Sampling frequency
1

window
Windowing function and number of samples to use for each section
Periodic Hamming window of length to obtain eight equal sections of x and y

noverlap
Number of samples by which the sections overlap
Value to obtain 50% overlap

Parameter	Description	Default Value
`nfft`	FFT length which determines the frequencies at which the coherence is estimated For real `x` and `y`, the length of `Cxy` is (`nfft`/2+1) if `nfft` is even or (`nfft`+1)/2 if `nfft` is odd. For complex `x` or `y`, the length of `Cxy` is `nfft`. If `nfft` is greater than the signal length, the data is zero-padded. If `nfft` is less than the signal length, the segment is wrapped using datawrap so that the length is equal to `nfft`.	Maximum of 256 or the next power of 2 greater than the length of each section of `x` or `y`
`fs`	Sampling frequency	1
`window`	Windowing function and number of samples to use for each section	Periodic Hamming window of length to obtain eight equal sections of x and `y`
`noverlap`	Number of samples by which the sections overlap	Value to obtain 50% overlap

Note You can use the empty matrix [] to specify the default value for any input argument except x or y. For example, Pxy = mschoere(x,y,[],[],128 uses a Hamming window, default noverlap to obtain 50% overlap, and the specified 128 nfft.

Cxy = mscohere(x,y,window) specifies a windowing function, divides x and y into equal overlapping sections of the specified window length, and windows each section using the specified window function. If you supply a scalar for window, Cxy uses a Hamming window of that length. mscohere zero pads the sections if the window length exceeds nfft.

Cxy = mscohere(x,y,window,noverlap) overlaps the sections of x by noverlap samples. noverlap must be an integer smaller than the length of window.

[Pxy,W] = mscohere(x,y,window,noverlap,nfft) uses the specified FFT length nfft to calculate the coherence estimate. It also returns W, which is the vector of normalized frequencies (in rad/sample) at which the coherence is estimated. For real x and y, Cxy length is (nfft/2 +1) if nfft is even and if nfft is odd, the length is (nfft+1)/2. For complex x or y, the length of Cxy is nfft. For real signals, the range of W is [0, pi] when nfft is even and [0, pi) when nfft is odd. For complex signals, the range of W is [0, 2*pi).

[Cxy,F] = mscohere(x,y,window,noverlap,nfft,fs) returns Cxy as a function of frequency and a vector F of frequencies at which the coherence is estimated. fs is the sampling frequency in Hz. For real signals, the range of F is [0, fs/2] when nfft is even and [0, fs/2) when nfft is odd. For complex signals, the range of F is [0, fs).

[...] = mscohere(x,y,...,'whole') returns a coherence estimate with frequencies that range over the whole Nyquist interval. Specifying 'half' uses half the Nyquist interval.

mscohere(...) plots the magnitude squared coherence versus frequency in the current figure window.

Note If you use mscohere on two linearly related signals [1] with a single, non-overlapping window, the output for all frequencies is Cxy = 1.

Examples

Compute and plot the coherence estimate between two colored noise sequences x and y:

randn('state',0);
h = fir1(30,0.2,rectwin(31));
h1 = ones(1,10)/sqrt(10);
r = randn(16384,1);
x = filter(h1,1,r);
y = filter(h,1,x);
mscohere(x,y,hanning(1024),512,1024)

Algorithm

mscohere estimates the magnitude squared coherence function [2] using Welch's averaged periodogram method (see references [3] and [4]).

References

[1] Stoica, P., and R. Moses. Introduction to Spectral Analysis. Upper Saddle River, NJ: Prentice-Hall, 1997. Pgs. 61-64.

[2] Kay, S.M. Modern Spectral Estimation. Englewood Cliffs, NJ: Prentice-Hall, 1988. Pg. 454.

[3] Rabiner, L.R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975.

[4] Welch, P.D. "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms." IEEE Trans. Audio Electroacoust. Vol. AU-15 (June 1967). Pgs. 70-73.

modulate nuttallwin