pwelch (Signal Processing Toolbox)

Power spectral density (PSD) using Welch's method

Syntax

[Pxx,w] = pwelch(x)
[Pxx,w] = pwelch(x,window)
[Pxx,w] = pwelch(x,window,noverlap)
[Pxx,w] = pwelch(x,window,noverlap,nfft)
[Pxx,f] = pwelch(x,window,noverlap,nfft,fs)
[...] = pwelch(x,window,noverlap,...,'range')
pwelch(...)

Description

Note pwelch computes the power spectral density, not the power spectrum. The difference between them is discussed in Spectral Analysis.

[Pxx,w] = pwelch(x) estimates the power spectral density Pxx of the input signal vector x using Welch's averaged modified periodogram method of spectral estimation. With this syntax:

The vector x is segmented into eight sections of equal length, each with 50% overlap.
Any remaining (trailing) entries in x that cannot be included in the eight segments of equal length are discarded.
Each segment is windowed with a Hamming window (see hamming) that is the same length as the segment.

The power spectral density is calculated in units of power per radians per sample. The corresponding vector of frequencies w is computed in radians per sample, and has the same length as Pxx.

A real-valued input vector x produces a full power one-sided (in frequency) PSD (by default), while a complex-valued x produces a two-sided PSD.

In general, the length N of the FFT and the values of the input x determine the length of Pxx and the range of the corresponding normalized frequencies. For this syntax, the (default) length N of the FFT is the larger of 256 and the next power of 2 greater than the length of the segment. The following table indicates the length of Pxx and the range of the corresponding normalized frequencies for this syntax.

PSD Vector Characteristics for an FFT Length of N (Default)
Real/Complex Input Data
Length of Pxx
Range of the Corresponding Normalized Frequencies

Real-valued
(N/2) +1
[0, ]

Complex-valued
N
[0, 2)

**PSD Vector Characteristics for an FFT Length of N (Default)**
Real/Complex Input Data	Length of Pxx	Range of the Corresponding Normalized Frequencies
Real-valued	(N/2) +1	[0, ]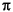
Complex-valued	N	[0, 2)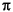

[Pxx,w] = pwelch(x,window) calculates the modified periodogram using either:

The window length window for the Hamming window when window is a positive integer
The window weights specified in window when window is a vector

With this syntax, the input vector x is divided into an integer number of segments with 50% overlap, and each segment is the same length as the window. Entries in x that are left over after it is divided into segments are discarded. If you specify window as the empty vector [], then the signal data is divided into eight segments, and a Hamming window is used on each one.

[Pxx,w] = pwelch(x,window,noverlap) divides x into segments according to window, and uses the integer noverlap to specify the number of signal samples (elements of x) that are common to two adjacent segments. noverlap must be less than the length of the window you specify. If you specify noverlap as the empty vector [], then pwelch determines the segments of x so that there is 50% overlap (default).

[Pxx,w] = pwelch(x,window,noverlap,nfft) uses Welch's method to estimate the PSD while specifying the length of the FFT with the integer nfft. If you set nfft to the empty vector [], it adopts the default value for N listed in the previous syntax.

The length of Pxx and the frequency range for w depend on nfft and the values of the input x. The following table indicates the length of Pxx and the frequency range for w for this syntax.

PSD and Frequency Vector Characteristics
Real/Complex Input Data
nfft Even/Odd
Length of Pxx
Range of w

Real-valued
Even
(nfft/2 + 1)
[0, ]

Real-valued
Odd
(nfft + 1)/2
[0, )

Complex-valued
Even or odd
nfft
[0, 2)

**PSD and Frequency Vector Characteristics**
Real/Complex Input Data	nfft Even/Odd	Length of Pxx	Range of w
Real-valued	Even	`(nfft/2 + 1)`	[0, ]
Real-valued	Odd	`(nfft + 1)/2`	[0, )
Complex-valued	Even or odd	`nfft`	[0, 2)

[Pxx,f] = pwelch(x,window,noverlap,nfft,fs) uses the sampling frequency fs specified in hertz (Hz) to compute the PSD vector (Pxx) and the corresponding vector of frequencies (f). In this case, the units for the frequency vector are in Hz. The spectral density produced is calculated in units of power per Hz. If you specify fs as the empty vector [], the sampling frequency defaults to 1 Hz.

The frequency range for f depends on nfft, fs, and the values of the input x. The length of Pxx is the same as in the Table , PSD and Frequency Vector Characteristics above. The following table indicates the frequency range for f for this syntax.

PSD and Frequency Vector Characteristics with fs Specified
Real/Complex Input Data
nfft Even/Odd
Range of f

Real-valued
Even
[0,fs/2]

Real-valued
Odd
[0,fs/2)

Complex-valued
Even or odd
[0,fs)

**PSD and Frequency Vector Characteristics with fs Specified**
Real/Complex Input Data	nfft Even/Odd	Range of f
Real-valued	Even	`[0,fs/2]`
Real-valued	Odd	`[0,fs/2)`
Complex-valued	Even or odd	`[0,fs)`

[...] = pwelch(x,window,noverlap,...,'range') specifies the range of frequency values. This syntax is useful when x is real. The string 'range' can be either:

'twosided': Compute the two-sided PSD over the frequency range [0,fs). This is the default for determining the frequency range for complex-valued x.

If you specify fs as the empty vector, [], the frequency range is [0,1).
If you don't specify fs, the frequency range is [0, 2).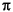

'onesided': Compute the one-sided PSD over the frequency ranges specified for real x. This is the default for determining the frequency range for real-valued x.

The string 'range' can appear anywhere in the syntax after noverlap.

pwelch(x,...) with no output arguments plots the PSD estimate in dB per unit frequency in the current figure window.

Examples

Estimate the PSD of a signal composed of a sinusoid plus noise, sampled at 1000 Hz. Use 33-sample windows with 32-sample overlap, and the default FFT length, and display the two-sided PSD estimate:

randn('state',0);
Fs = 1000;   t = 0:1/Fs:.3;
x = cos(2*pi*t*200) + randn(size(t));  % 200Hz cosine plus noise
pwelch(x,33,32,[],Fs,'twosided')

Algorithm

pwelch calculates the power spectral density using Welch's method (see references):

The input signal vector x is divided into k overlapping segments according to window and noverlap (or their default values).
The specified (or default) window is applied to each segment of x.
An nfft-point FFT is applied to the windowed data.
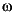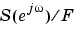The (modified) periodogram of each windowed segment is computed.
The set of modified periodograms is averaged to form the spectrum estimate S(e^j).
The resulting spectrum estimate is scaled to compute the power spectral density as , where F is

2 when you do not supply the sampling frequency
fs when you supply the sampling frequency

The number of segments k that x is divided into is calculated as:

Eight if you don't specify window, or if you specify it as the empty vector []
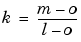if you specify window as a nonempty vector or a scalar

In this equation, m is the length of the signal vector x, o is the number of overlapping samples (noverlap), and l is the length of each segment (the window length).

See Also

dspdata.msspectrum, pburg, pcov, peig, periodogram, pmcov, pmtm, pmusic, pyulear

References

[1] Hayes, M., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, 1996.

[2] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, Englewood Cliffs, NJ, 1997, pp. 52-54.

[3] Welch, P.D, "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms," IEEE Trans. Audio Electroacoustics, Vol. AU-15 (June 1967), pp. 70-73.

pulstran pyulear