Wavelet Toolbox

Wavelet Reconstruction

We've learned how the discrete wavelet transform can be used to analyze, or decompose, signals and images. This process is called decomposition or analysis. The other half of the story is how those components can be assembled back into the original signal without loss of information. This process is called reconstruction, or synthesis. The mathematical manipulation that effects synthesis is called the inverse discrete wavelet transform (IDWT).

To synthesize a signal in the Wavelet Toolbox, we reconstruct it from the wavelet coefficients:

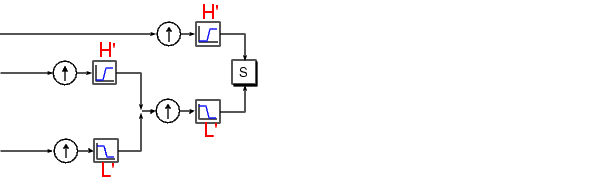
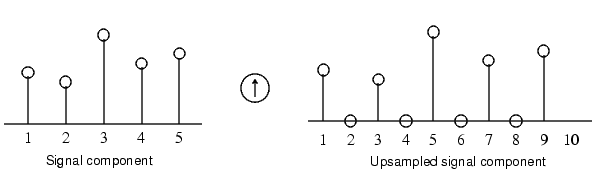
Where wavelet analysis involves filtering and downsampling, the wavelet reconstruction process consists of upsampling and filtering. Upsampling is the process of lengthening a signal component by inserting zeros between samples:

The Wavelet Toolbox includes commands, like idwt and waverec, that perform single-level or multilevel reconstruction, respectively, on the components of one-dimensional signals. These commands have their two-dimensional analogs, idwt2 and waverec2.

Multiple-Level Decomposition

Reconstruction Filters

© 1994-2005 The MathWorks, Inc.