Wavelet Toolbox

De-Noising a Signal Using Wavelet Packets

We now use the Wavelet Packet 1-D tool to analyze a noisy chirp signal. This analysis illustrates the use of Stein's Unbiased Estimate of Risk (SURE) as a principle for selecting a threshold to be used for de-noising.

This technique calls for setting the threshold T to

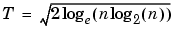
where n is the length of the signal.

A more thorough discussion of the SURE criterion appears in Choosing the Optimal Decomposition. For now, suffice it to say that this method works well if your signal is normalized in such a way that the data fit the model x(t) = f(t) + e(t), where e(t) is a Gaussian white noise with zero mean and unit variance.

If you've already started the Wavelet Packet 1-D tool and it is active on your computer's desktop, skip ahead to step 3.

Starting the Wavelet Packet 1-D Tool.   

1. From the MATLAB prompt, type wavemenu.

1. The Wavelet Toolbox Main Menu appears.

   

   Click the Wavelet Packet 1-D menu item.

   The tool appears on the desktop.

   

Loading a Signal.   

2. From the File menu, choose the Load Signal option.

   

3. When the Load Signal dialog box appears, select the demo MAT-file noischir.mat, which should reside in the MATLAB directory toolbox/wavelet/wavedemo. Click the OK button.

   

1. The noischir signal is loaded into the Wavelet Packet 1-D tool. Notice that the signal's length is 1024. This means we should set the SURE criterion threshold equal to sqrt(2.*log(1024.*log2(1024))), or 4.2975.

   

Analyzing a Signal.   

4. Make the appropriate settings for the analysis. Select the db2 wavelet, level 4, entropy type sure, and threshold parameter 4.2975. Click the Analyze button.

   

1. There is a pause while the wavelet packet analysis is computed.

Note    Many capabilities are available using the command area on the right of the Wavelet Packet 1-D window. Some of them are used in the sequel. For a more complete description, see Wavelet Packet Tool Features (1-D and 2-D).

Computing the Best Tree and Performing De-Noising.   

5. Click the Best Tree button.

1. Computing the best tree makes the de-noising calculations more efficient.

   

6. Click the De-noise button. This brings up the Wavelet Packet 1-D De-Noising window.

   

7. Click the De-noise button located at the center right side of the Wavelet Packet 1-D De-Noising window.

The results of the de-noising operation are quite good, as can be seen by looking at the thresholded coefficients. The frequency of the chirp signal increases quadratically over time, and the thresholded coefficients essentially capture the quadratic curve in the time-frequency plane.

You can also use the wpdencmp function to perform wavelet packet de-noising or compression from the command line.

Compressing a Signal Using Wavelet Packets

Two-Dimensional Wavelet Packet Analysis

© 1994-2005 The MathWorks, Inc.