wpdencmp (Wavelet Toolbox)

De-noising or compression using wavelet packets

Syntax

[XD,TREED,PERF0,PERFL2] = 
wpdencmp(X,SORH,N,'wname',CRIT,PAR,KEEPAPP)
[XD,TREED,PERF0,PERFL2] =        
wpdencmp(TREE,SORH,CRIT,PAR,KEEPAPP)

Description

wpdencmp is a one- or two-dimensional de-noising and compression oriented function.

wpdencmp performs a de-noising or compression process of a signal or an image, using wavelet packet. The ideas and the procedures for de-noising and compression using wavelet packet decomposition are the same as those used in the wavelets framework (see wden and wdencmp for more information).

[XD,TREED,PERF0,PERFL2] = wpdencmp(X,SORH,N,'wname',CRIT,PAR,KEEPAPP) returns a de-noised or compressed version XD of input signal X (one- or two-dimensional) obtained by wavelet packets coefficients thresholding.

The additional output argument TREED is the wavelet packet best tree decomposition (see besttree for more information) of XD. PERFL2 and PERF0 are L² energy recovery and compression scores in percentages.

PERFL2 = 100 * (vector-norm of WP-cfs of XD / vector-norm of WP-cfs of X)².

If X is a one-dimensional signal and 'wname' an orthogonal wavelet, PERFL2 is reduced to

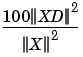
SORH ('s' or 'h') is for soft or hard thresholding (see wthresh for more information).

Wavelet packet decomposition is performed at level N and 'wname' is a string containing the wavelet name. Best decomposition is performed using entropy criterion defined by string CRIT and parameter PAR (see wentropy for more information). Threshold parameter is also PAR. If KEEPAPP = 1, approximation coefficients cannot be thresholded; otherwise, they can be.

[XD,TREED,PERF0,PERFL2] = wpdencmp(TREE,SORH,CRIT,PAR,KEEPAPP) has the same output arguments, using the same options as above, but obtained directly from the input wavelet packet tree decomposition TREE (see wpdec for more information) of the signal to be de-noised or compressed.

In addition if CRIT = 'nobest' no optimization is done and the current decomposition is thresholded.

Examples

% The current extension mode is zero-padding (see dwtmode).

% Load original signal. 
load sumlichr; x = sumlichr;

% Use wpdencmp for signal compression. 
% Find default values (see ddencmp). 
[thr,sorh,keepapp,crit] = ddencmp('cmp','wp',x)

thr =
    0.5193

sorh =
h

keepapp =
    1

crit =
    threshold

% De-noise signal using global thresholding with 
% threshold best basis. 
[xc,treed,datad,perf0,perfl2] = ... 
wpdencmp(x,sorh,3,'db2',crit,thr,keepapp);

% Using some plotting commands,
% the following figure is generated.


% Load original image. 
load sinsin

% Generate noisy image. 
init = 2055615866; randn('seed',init); 
x = X/18 + randn(size(X));

% Use wpdencmp for image de-noising. 
% Find default values (see ddencmp).
[thr,sorh,keepapp,crit] = ddencmp('den','wp',x)

thr =
    4.9685

sorh =
h
keepapp =
    1

crit =
sure    
% De-noise image using global thresholding with 
% SURE best basis. 
xd = wpdencmp(x,sorh,3,'sym4',crit,thr,keepapp);

% Using some plotting commands,
% the following figure is generated.



% Generate heavy sine and a noisy version of it.
[xref,x] = wnoise(5,11,7,init);

% Use wpdencmp for signal de-noising. 
n = length(x); 
thr = sqrt(2*log(n*log(n)/log(2))); 
xwpd = wpdencmp(x,'s',4,'sym4','sure',thr,1);

% Compare with wavelet-based de-noising result. 
xwd = wden(x,'rigrsure','s','one',4,'sym4');

% Using some plotting commands,
% the following figure is generated.

See Also

besttree, ddencmp, wdencmp, wenergy, wpbmpen, wpdec, wpdec2, wthresh

References

Antoniadis, A.; G. Oppenheim, Eds. (1995), Wavelets and statistics, Lecture Notes in Statistics, 103, Springer Verlag.

Coifman, R.R.; M.V. Wickerhauser (1992), "Entropy-based algorithms for best basis selection," IEEE Trans. on Inf. Theory, vol. 38, 2, pp. 713-718.

DeVore, R.A.; B. Jawerth, B.J. Lucier (1992), "Image compression through wavelet transform coding," IEEE Trans. on Inf. Theory, vol. 38, No 2, pp. 719-746.

Donoho, D.L. (1993), "Progress in wavelet analysis and WVD: a ten minute tour," in Progress in wavelet analysis and applications, Y. Meyer, S. Roques, pp. 109-128. Frontières Ed.

Donoho, D.L.; I.M. Johnstone (1994), "Ideal spatial adaptation by wavelet shrinkage," Biometrika, vol 81, pp. 425-455.

Donoho, D.L.; I.M. Johnstone, G. Kerkyacharian, D. Picard (1995), "Wavelet shrinkage: asymptopia," Jour. Roy. Stat. Soc., series B, vol. 57 no. 2, pp. 301-369.

wpdec2 wpfun