| Wavelet Toolbox | |
Wavelet Packets in Action: an Introduction
The following simple examples illustrate certain differences between wavelet analysis and wavelet packet analysis.
Example 1: Analyzing a Sine Function
The signal to be analyzed, called sinper8, is a 256-length sampled sine function of period 8. The Haar wavelet is used to decompose the signal at level 7.
The following figure contains the "time-frequency" plot (x-axis is time and y-axis is frequency, high to low from the top to the bottom) for the wavelet decomposition (on the left) and for the wavelet packet decomposition (on the right).
Wavelet decomposition localizes the period of the sine within the interval [8,16]. Wavelet packets provide a more precise estimation of the actual period.
How to Obtain and Explain These Graphs?.
You can reproduce these graphs by typing at the MATLAB prompt
Then click the Wavelet Packet 1-D option and select the Example Analysis using the sinper8 demo signal. For more information on using this GUI tool, see the section One-Dimensional Wavelet Packet Analysis.
The length of the WP tree leaves is 2; there are 128 leaves, labeled from (7,0) to (7,127) and indexed from 127 to 254.
The associated wavelet tree (click the Wavelet Tree button) is obviously simpler than the wavelet packet tree. There are eight leaves labeled (7,0), (7,1), (6,1), . . . (2,1), (1,1).
The Colored Coefficients for Terminal Nodes graph deserves explanation. In principle the graphic displays eight stripes. When using Global + abs, only four seem to be present. In fact, the eight are drawn. As the values of several coefficients are close to 0, the stripes are merged and only four can be seen. The eight stripes are recovered when using the option By level + abs.
Getting back to the Colored Coefficients for Terminal Nodes graph of the initial tree, with cool colormap, two stripes are present. By zooming in, we determine their WP index or position:
Using the two sliders of the Decomposition Tree graphic, we can visualize the coefficients or the reconstructed signals corresponding to these four leaves.
Figure 6-35: Wavelets (Left) Versus Wavelet Packets (Right): a Sine Function
Example 2: Analyzing a Chirp Signal
The signal to be analyzed is a chirp: an oscillatory signal with increasing modulation sin (250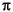
t2) sampled 512 times on [0, 1]. For this "linear" chirp, the derivative of the phase is linear. On the left of Figure 6-36, a wavelet analysis does not easily detect this time-frequency property of the signal. But on the right of Figure 6-36, the linear slope for the greatest wavelet packet coefficients in absolute value is obvious. The same experiment can be done with a "quadratic" chirp of the form sin (k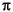t3) in which the greatest wavelet packet coefficients exhibit a quadratic time frequency pattern.
Figure 6-36: Wavelets (Left) Versus Wavelet Packets (Right): Damped Oscillations
| | From Wavelets to Wavelet Packets: Decomposing the Details | Building Wavelet Packets | |
© 1994-2005 The MathWorks, Inc.
