Wavelet Toolbox

Building Wavelet Packets

The computation scheme for wavelet packets generation is easy when using an orthogonal wavelet. We start with the two filters of length 2N, where h(n) and g(n), corresponding to the wavelet.

Now by induction let us define the following sequence of functions:

• (W_n(x), n = 0, 1, 2, ...)

by

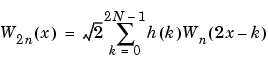
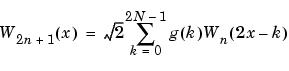
where W₀(x) = 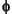(x) is the scaling function and W₁(x) = 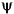(x) is the wavelet function.

For example for the Haar wavelet we have

and

The equations become

and

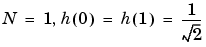
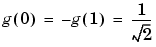
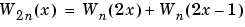
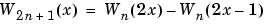
W₀(x) = 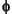(x) is the Haar scaling function and W₁(x) = 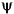(x) is the Haar wavelet, both supported in [0, 1]. Then we can obtain W_2n by adding two 1/2-scaled versions of W_n with distinct supports [0,1/2] and [1/2,1] and obtain W_2n+1 by subtracting the same versions of W_n.

For n = 0 to 7, we have the W-functions shown below.

Figure 6-37: The Haar Wavelet Packets

This can be obtained using the following command:

• [wfun,xgrid] = wpfun('db1',7,5);
  

which returns in wfun the approximate values of W_n for n = 0 to 7, computed on

a 1/2⁵ grid of the support xgrid.

Starting from more regular original wavelets and using a similar construction, we obtain smoothed versions of this system of W-functions, all with support in the interval [0, 2N-1]. Figure 6-38, below, presents the system of W-functions for the original db2 wavelet.

Figure 6-38: The db2 Wavelet Packets

Wavelet Packets in Action: an Introduction

Wavelet Packet Atoms

© 1994-2005 The MathWorks, Inc.