| Wavelet Toolbox | |
Starting from the functions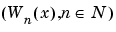 
and following the same line leading to orthogonal wavelets, we consider the three-indexed family of analyzing functions (the waveforms):
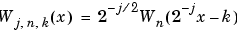
As in the wavelet framework, k can be interpreted as a time-localization parameter and j as a scale parameter. So what is the interpretation of n?
The basic idea of the wavelet packets is that for fixed values of j and k, Wj,n,k analyzes the fluctuations of the signal roughly around the position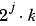 
, at the scale 
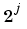and at various frequencies for the different admissible values of the last parameter n.
In fact, examining carefully the wavelet packets displayed in Figure 6-37 and Figure 6-38, the naturally ordered Wn for n = 0, 1, ..., 7, does not match exactly the order defined by the number of oscillations. More precisely, counting the number of zero crossings (up-crossings and down-crossings) for the db1 wavelet packets, we have the following.
| Natural order n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Number of zero crossings for db1 Wn |
2 |
3 |
5 |
4 |
9 |
8 |
6 |
7 |
So, to restore the property that the main frequency increases monotonically with the order, it is convenient to define the frequency order obtained from the natural one recursively.
| Natural order n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Frequency order r(n) |
0 |
1 |
3 |
2 |
6 |
7 |
5 |
4 |
As can be seen in the previous figures, Wr(n)(x) "oscillates" approximately n times.
To analyze a signal (the chirp of example 2 for instance), it is better to plot the wavelet packet coefficients following the Frequency order (on the right of Figure 6-39) from the low frequencies at the bottom to the high frequencies at the top, rather than naturally ordered coefficients (on the left of Figure 6-39).
Figure 6-39: Natural and Frequency Ordered Wavelet Packets Coefficients
When plotting the coefficients, the various options related to the "Frequency" or "Natural" order choice are available using the GUI tools.
These options are also available from the command line mode when using the wpviewcf function.
| | Building Wavelet Packets | Organizing the Wavelet Packets | |
© 1994-2005 The MathWorks, Inc.
and 
.