Local and Global Analysis :: Advanced Concepts (Wavelet Toolbox)

Wavelet Toolbox

Local and Global Analysis

A small scale value permits us to perform a local analysis; a large scale value is used for a global analysis. Combining local and global is a useful feature of the method. Let us be a bit more precise about the local part and glance at the frequency domain counterpart.

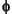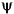Imagine that the analyzing function phi or psi is zero outside of a domain U, which is contained in a disk of radius 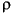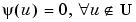rho : . The wavelet 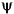psi is localized. The signal s and the function 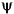psi are then compared in the disk, taking into account only the t values in the disk. The signal values, which are located outside of the domain U, do not influence the value of the coefficient

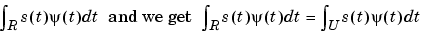
The same argument holds when 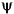psi is translated to position b and the corresponding coefficient analyzes s around b. So this analysis is local.

The wavelets having a compact support are used in local analysis. This is the case for Haar and Daubechies wavelets, for example. The wavelets whose values are considered as very small outside a domain U can be used with caution, as if they were in fact actually zero outside U. Not every wavelet has a compact support. This is the case, for instance, of the Meyer wavelet.

The previous localization is temporal, and is useful in analyzing a temporal signal (or spatial signal if analyzing an image). The good spectral domain localization is a second type of a useful property. A result (linked to the Heisenberg uncertainty principle) links the dispersion of the signal f and the dispersion of its Fourier transform 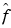, and therefore of the dispersion of 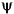psi and 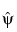. The product of these dispersions is always greater than a constant c (which does not depend on the signal, but only on the dimension of the space). So it is impossible to reduce arbitrarily both time and frequency localization.

In the Fourier and spectral analysis, the basic function is 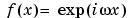. This function is not a time localized function. The support is R. Its Fourier transform 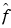is a generalized function concentrated at point .

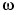The function f is very poorly localized in time, but 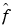is perfectly localized in frequency. The wavelets generate an interesting "compromise" on the supports, and this compromise differs from that of complex exponentials, sine, or cosine.

Wavelet Transforms: Continuous and Discrete Synthesis: An Inverse Transform