Wavelet Toolbox

Wavelet Transforms: Continuous and Discrete

The wavelet transform of a signal s is the family C(a,b), which depends on two indices a and b. The set to which a and b belong is given below in the table. The studies focus on two transforms:

• Continuous transform
• Discrete transform

From an intuitive point of view, the wavelet decomposition consists of calculating a "resemblance index" between the signal and the wavelet located at position b and of scale a. If the index is large, the resemblance is strong, otherwise it is slight. The indexes C(a,b) are called coefficients.

We define the coefficients in the following table. We have two types of analysis at our disposal.

Continuous Time Signal Continuous Analysis	Continuous Time Signal Discrete Analysis

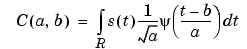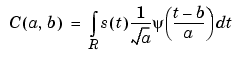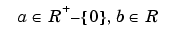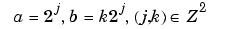Next we will illustrate the differences between the two transforms, for the analysis of a fractal signal (see the following figure).

Figure 6-6: Continuous Versus Discrete Transform

Using a redundant representation close to the so-called continuous analysis, instead of a nonredundant discrete time-scale representation, can be useful for analysis purposes. The nonredundant representation is associated with an orthonormal basis, whereas the redundant representation uses much more scale and position values than a basis. For a classical fractal signal, the redundant methods are quite accurate.

• Graphic representation of discrete analysis: (in the middle of Figure 6-6, Continuous Versus Discrete Transform) time is on the abscissa and on the ordinate the scale a is dyadic: 2¹, 2², 2³, 2⁴, and 2⁵ (from the bottom to the top), levels are 1, 2, 3, 4, and 5. Each coefficient of level k is repeated 2^k times.
• Graphic representation of continuous analysis: (at the bottom of Figure 6-6, Continuous Versus Discrete Transform) time is on the abscissa and on the ordinate the scale varies almost continuously between 2¹ and 2⁵ by step 1 (from the bottom to the top). Keep in mind that when a scale is small, only small details are analyzed, as in a geographical map.

Wavelets and Associated Families

Local and Global Analysis

© 1994-2005 The MathWorks, Inc.