Wavelet Toolbox

Synthesis: An Inverse Transform

In order to be efficient and useful, a method designed for analysis also has to be able to perform synthesis. The wavelet method achieves this.

The analysis starts from s and results in the coefficients C(a,b). The synthesis starts from the coefficients C(a,b) and reconstructs s. Synthesis is the reciprocal operation of analysis.

For signals of finite energy, there are two formulas to perform the inverse wavelet transform:

• Continuous synthesis:

• where is a constant depending on .

• Discrete synthesis:

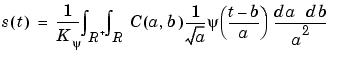
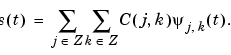
Of course, the previous formulas need some hypotheses on the 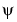function. More precisely, see What Functions Are Candidates to Be a Wavelet? for the continuous synthesis formula and Why Does Such an Algorithm Exist? for the discrete one.

Local and Global Analysis

Details and Approximations

© 1994-2005 The MathWorks, Inc.