Wavelet Toolbox

Details and Approximations

The equations for continuous and discrete synthesis are of considerable interest and can be read in order to define the detail at level j:

1. Let us fix j and sum on k. A detail is nothing more than the function

2. Now, let us sum on j. The signal is the sum of all the details:

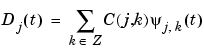
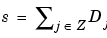
The details have just been defined. Take a reference level called J. There are two sorts of details. Those associated with indices 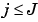correspond to the scales 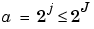which are the fine details. The others, which correspond to j > J, are the coarser details.

We group these latter details into

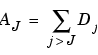
which defines what is called an approximation of the signal s. We have just created the details and an approximation. They are connected. The equality

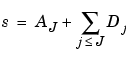
signifies that s is the sum of its approximation A_J and of its fine details. From the previous formula, it is obvious that the approximations are related to one another by

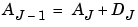
For an orthogonal analysis, in which the 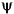_j,k is an orthonormal family,

• A_J is orthogonal to D_J, D_J-1, D_J-2, ...

• s is the sum of the two orthogonal signals: A_J and
  
  

• A_J is an approximation of s. The quality (in energy) of the approximation of s
  by A_J is

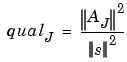
The following table contains definitions of details and approximations.

Definition of the detail at level j
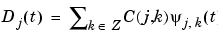The signal is the sum of its details
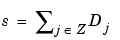The approximation at level J
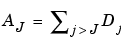Link between AJ-1 and AJ	AJ-1 = AJ + DJ
Several decompositions

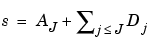From a graphical point of view, when analyzing a signal, it is always valuable to represent the different signals (s, A_j, D_j) and coefficients (C(j,k)).

Let us consider the following figure. On the left side, s is the signal; a5, a4, a3, a2, and a1 are the approximations at levels 5, 4, 3, 2, and 1. The best approximation is a1; the next one is a2, and so on. Noise oscillations are exhibited in a1, whereas a5 is smoother.

On the right side, cfs represents the coefficients (for more information, see Wavelet Transforms: Continuous and Discrete), s is the signal, and d5, d4, d3, d2, and d1 are the details at levels 5, 4, 3, 2, and 1.

The different signals that are presented exist in the same time grid. We can consider that the t index of detail D₄(t) identifies the same temporal instant as that of the approximation A₅(t) and that of the signal s(t). This identity is of considerable practical interest in understanding the composition of the signal, even if the wavelet sometimes introduces dephasing.

Figure 6-7: Approximations, Details, and Coefficients

Synthesis: An Inverse Transform

The Fast Wavelet Transform (FWT) Algorithm

© 1994-2005 The MathWorks, Inc.