wpbmpen (Wavelet Toolbox)

Penalized threshold for wavelet packet de-noising

Syntax

THR = wpbmpen(T,SIGMA,ALPHA)
THR = wpbmpen(T,SIGMA,ALPHA,ARG)

Description

THR = wpbmpen(T,SIGMA,ALPHA) returns a global threshold THR for de-noising. THR is obtained by a wavelet packet coefficients selection rule using a penalization method provided by Birge-Massart.

T is a wavelet packet tree corresponding to the wavelet packet decomposition of the signal or image to be de-noised.

SIGMA is the standard deviation of the zero mean Gaussian white noise in the de-noising model (see wnoisest for more information).

ALPHA is a tuning parameter for the penalty term. It must be a real number greater than 1. The sparsity of the wavelet packet representation of the de-noised signal or image grows with ALPHA. Typically ALPHA = 2.

THR minimizes the penalized criterion given by

let t^* be the minimizer of

crit(t) = -sum(c(k)^2,kt) + 2*SIGMA^2*t*(ALPHA + log(n/t))

where c(k) are the wavelet packet coefficients sorted in decreasing order of their absolute value and n is the number of coefficients, then THR = 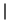c(t^*).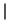

wpbmpen(T,SIGMA,ALPHA,ARG) computes the global threshold and, in addition, plots three curves:

2*SIGMA^2*t*(ALPHA + log(n/t))
sum(c(k)^2,kt)
crit(t).

Examples

% Example 1: Signal de-noising.
% Load noisy chirp signal.
load noischir; x = noischir;

% Perform a wavelet packet decomposition of the signal
% at level 5 using sym6.
wname = 'sym6'; lev = 5;
tree = wpdec(x,lev,wname);

% Estimate the noise standard deviation from the
% detail coefficients at level 1,
% corresponding to the node index 2.
det1 = wpcoef(tree,2);
sigma = median(abs(det1))/0.6745;

% Use wpbmpen for selecting global threshold  
% for signal de-noising, using the recommended parameter.
alpha = 2;
thr = wpbmpen(tree,sigma,alpha)

thr =

    4.5740


% Use wpdencmp for de-noising the signal using the above
% threshold with soft thresholding and keeping the approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);

% Plot original and de-noised signals.
figure(1)
subplot(211), plot(x),
title('Original signal')
subplot(212), plot(xd)
title('De-noised signal')


% Example 2: Image de-noising.
% Load original image.
load noiswom; 
nbc = size(map,1);

% Perform a wavelet packet decomposition of the image
% at level 3 using coif2.
wname = 'coif2'; lev = 3;
tree = wpdec2(X,lev,wname);
      
% Estimate the noise standard deviation from the
% detail coefficients at level 1.
det1 = [wpcoef(tree,2) wpcoef(tree,3) wpcoef(tree,4)];
sigma = median(abs(det1(:)))/0.6745;

% Use wpbmpen for selecting global threshold  
% for image de-noising.
alpha = 1.1;
thr = wpbmpen(tree,sigma,alpha)

thr =

   38.5125


% Use wpdencmp for de-noising the image using the above
% thresholds with soft thresholding and keeping the 
approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);

% Plot original and de-noised images.
figure(2)
colormap(pink(nbc));
subplot(221), image(wcodemat(X,nbc))
title('Original image')
subplot(222), image(wcodemat(xd,nbc))
title('De-noised image')

See Also
wbmpen, wden, wdencmp, wpdencmp

wp2wtree wpcoef