wpfun (Wavelet Toolbox)

Wavelet packet functions

Syntax

[WPWS,X] = wpfun('wname',NUM,PREC)
[WPWS,X] = wpfun('wname',NUM)

Description

wpfun is a wavelet packet analysis function.

[WPWS,X] = wpfun('wname',NUM,PREC) computes the wavelet packets for a wavelet 'wname' (see wfilters for more information), on dyadic intervals of length 2^-PREC.

PREC must be a positive integer. Output matrix WPWS contains the W functions of index from 0 to NUM, stored row-wise as [W₀; W₁; ... ; W_NUM]. Output vector X is the corresponding common X-grid vector.

[WPWS,X] = wpfun('wname',NUM) is equivalent to [WPWS,X] = wpfun('wname',NUM,7).

The computation scheme for wavelet packets generation is easy when using an orthogonal wavelet. We start with the two filters of length 2N, denoted h(n) and g(n), corresponding to the wavelet.

Now by induction let us define the following sequence of functions (W_n(x) , n = 0,1,2,...) by

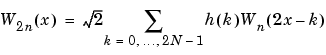
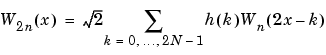
where W₀(x) = 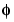(x) is the scaling function and W₁(x) = 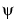(x) is the wavelet function.

For example for the Haar wavelet we have

and

The equations become

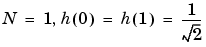
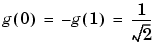
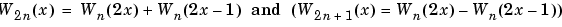
W₀(x) = 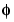(x) is the haar scaling function and W₁(x) = 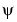(x) is the haar wavelet, both supported in [0,1].

Then we can obtain W₂_n by adding two 1/2-scaled versions of W_n with distinct supports [0,1/2] and [1/2,1], and obtain W₂_n₊₁ by subtracting the same versions of W_n.

Starting from more regular original wavelets, using a similar construction, we obtain smoothed versions of this system of W-functions, all with support in the interval [0, 2N-1].

Examples

% Compute the db2 Wn functions for n = 0 to 7, generating 
% the db2 wavelet packets. 
[wp,x] = wpfun('db2',7);

% Using some plotting commands,
% the following figure is generated.

See Also
wavefun, waveinfo

References

Coifman, R.R.; M.V. Wickerhauser (1992), "Entropy-based Algorithms for best basis selection," IEEE Trans. on Inf. Theory, vol. 38, 2, pp. 713-718.

Meyer, Y. (1993), Les ondelettes. Algorithmes et applications, Colin Ed., Paris, 2nd edition. (English translation: Wavelets: Algorithms and applications, SIAM).

Wickerhauser, M.V. (1991), "INRIA lectures on wavelet packet algorithms," Proceedings ondelettes et paquets d'ondes 17-21 June Rocquencourt France, pp. 31-99.

Wickerhauser, M.V. (1994), Adapted wavelet analysis from theory to software algorithms, A.K. Peters.

wpdencmp wpjoin