

| Mathematics |   |
Questions and Answers, and Troubleshooting
This section contains a number of tables that answer questions about the use and operation of the ODE solvers:
| Question |
Answer |
How do the ODE solvers differ from quad or quadl? |
quad and quadl solve problems of the form 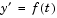 . The ODE solvers handle more general problems . The ODE solvers handle more general problems 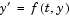 , linearly implicit problems that involve a mass matrix , linearly implicit problems that involve a mass matrix 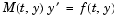 , and fully implicit problems , and fully implicit problems 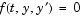 . . |
| Can I solve ODE systems in which there are more equations than unknowns, or vice versa? |
No. |
| Question |
Answer |
| How large a problem can I solve with the ODE suite? |
The primary constraints are memory and time. At each time step, the solvers for nonstiff problems allocate vectors of length n, where n is the number of equations in the system. The solvers for stiff problems but also allocate an n-by-n Jacobian matrix. For these solvers it may be advantageous to use the sparse option.If the problem is nonstiff, or if you are using the sparse option, it may be possible to solve a problem with thousands of unknowns. In this case, however, storage of the result can be problematic. Try asking the solver to evaluate the solution at specific points only, or call the solver with no output arguments and use an output function to monitor the solution. |
I'm solving a very large system, but only care about a couple of the components of y. Is there any way to avoid storing all of the elements? |
Yes. The user-installable output function capability is designed specifically for this purpose. When you call the solver with no output arguments, the solver does not allocate storage to hold the entire solution history. Instead, the solver calls OutputFcn(t,y,flag) at each time step. To keep the history of specific elements, write an output function that stores or plots only the elements you care about. |
| What is the startup cost of the integration and how can I reduce it? |
The biggest startup cost occurs as the solver attempts to find a step size appropriate to the scale of the problem. If you happen to know an appropriate step size, use the InitialStep property. For example, if you repeatedly call the integrator in an event location loop, the last step that was taken before the event is probably on scale for the next integration. See ballode for an example. |
| Question |
Answer |
| The first step size that the integrator takes is too large, and it misses important behavior. |
You can specify the first step size with the InitialStep property. The integrator tries this value, then reduces it if necessary. |
| Can I integrate with fixed step sizes? |
No. |
| Question |
Answer |
How do I choose RelTol and AbsTol? |
RelTol, the relative accuracy tolerance, controls the number of correct digits in the answer. AbsTol, the absolute error tolerance, controls the difference between the answer and the solution. At each step, the error e in component i of the solution satisfies |e(i)| <= max(RelTol*abs(y(i)),AbsTol(i))Roughly speaking, this means that you want RelTol correct digits in all solution components except those smaller than thresholds AbsTol(i). Even if you are not interested in a component y(i) when it is small, you may have to specify AbsTol(i) small enough to get some correct digits in y(i) so that you can accurately compute more interesting components. |
I want answers that are correct to the precision of the computer. Why can't I simply set RelTol to eps? |
You can get close to machine precision, but not that close. The solvers do not allow RelTol near eps because they try to approximate a continuous function. At tolerances comparable to eps, the machine arithmetic causes all functions to look discontinuous. |
| How do I tell the solver that I don't care about getting an accurate answer for one of the solution components? |
You can increase the absolute error tolerance corresponding to this solution component. If the tolerance is bigger than the component, this specifies no correct digits for the component. The solver may have to get some correct digits in this component to compute other components accurately, but it generally handles this automatically. |
| Question |
Answer |
| Can the solvers handle partial differential equations (PDEs) that have been discretized by the method of lines? |
Yes, because the discretization produces a system of ODEs. Depending on the discretization, you might have a form involving mass matrices - the ODE solvers provide for this. Often the system is stiff. This is to be expected when the PDE is parabolic and when there are phenomena that happen on very different time scales such as a chemical reaction in a fluid flow. In such cases, use one of the four solvers: ode15s, ode23s, ode23t, ode23tb. If there are many equations, set the JPattern property. This might make the difference between success and failure due to the computation being too expensive. For an example that uses JPattern, see Example: Large, Stiff, Sparse Problem. When the system is not stiff, or not very stiff, ode23 or ode45 is more efficient than ode15s, ode23s, ode23t, or ode23tb.Parabolic-elliptic partial differential equations in 1-D can be solved directly with the MATLAB PDE solver, pdepe. For more information, see Partial Differential Equations. |
| Can I solve differential-algebraic equation (DAE) systems? |
Yes. The solvers ode15s and ode23t can solve some DAEs of the form 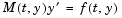 where where 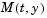 is singular. The DAEs must be of index 1. is singular. The DAEs must be of index 1. ode15i can solve fully implicit DAEs of index 1, 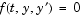 . For examples, see . For examples, see amp1dae, hb1dae, or ihb1dae. |
| Can I integrate a set of sampled data? |
Not directly. You have to represent the data as a function by interpolation or some other scheme for fitting data. The smoothness of this function is critical. A piecewise polynomial fit like a spline can look smooth to the eye, but rough to a solver; the solver takes small steps where the derivatives of the fit have jumps. Either use a smooth function to represent the data or use one of the lower order solvers (ode23, ode23s, ode23t, ode23tb) that is less sensitive to this. |
| What do I do when I have the final and not the initial value? |
All the solvers of the ODE suite allow you to solve backwards or forwards in time. The syntax for the solvers is[t,y] = ode45(odefun,[t0 tf],y0);and the syntax accepts t0 > tf. |
| Question |
Answer |
| The solution doesn't look like what I expected. |
If you're right about its appearance, you need to reduce the error tolerances from their default values. A smaller relative error tolerance is needed to compute accurately the solution of problems integrated over "long" intervals, as well as solutions of problems that are moderately unstable. You should check whether there are solution components that stay smaller than their absolute error tolerance for some time. If so, you are not asking for any correct digits in these components. This may be acceptable for these components, but failing to compute them accurately may degrade the accuracy of other components that depend on them. |
| My plots aren't smooth enough. |
Increase the value of Refine from its default of 4 in ode45 and 1 in the other solvers. The bigger the value of Refine, the more output points. Execution speed is not affected much by the value of Refine. |
| I'm plotting the solution as it is computed and it looks fine, but the code gets stuck at some point. |
First verify that the ODE function is smooth near the point where the code gets stuck. If it isn't, the solver must take small steps to deal with this. It may help to break tspan into pieces on which the ODE function is smooth.If the function is smooth and the code is taking extremely small steps, you are probably trying to solve a stiff problem with a solver not intended for this purpose. Switch to ode15s, ode23s, ode23t, or ode23tb. |
| My integration proceeds very slowly, using too many time steps. |
First, check that your tspan is not too long. Remember that the solver uses as many time points as necessary to produce a smooth solution. If the ODE function changes on a time scale that is very short compared to the tspan, the solver uses a lot of time steps. Long-time integration is a hard problem. Break tspan into smaller pieces.If the ODE function does not change noticeably on the tspan interval, it could be that your problem is stiff. Try using ode15s, ode23s, ode23t, or ode23tb.Finally, make sure that the ODE function is written in an efficient way. The solvers evaluate the derivatives in the ODE function many times. The cost of numerical integration depends critically on the expense of evaluating the ODE function. Rather than recompute complicated constant parameters at each evaluation, store them in globals or calculate them once and pass them to nested functions. |
I know that the solution undergoes a radical change at time t wherebut the integrator steps past without "seeing" it. |
If you know there is a sharp change at time t, it might help to break the tspan interval into two pieces, [t0 t] and [t tf], and call the integrator twice.If the differential equation has periodic coefficients or solution, you might restrict the maximum step size to the length of the period so the integrator won't step over periods. |
 | Examples: Applying the ODE Initial Value Problem Solvers | Initial Value Problems for DDEs |  |
© 1994-2005 The MathWorks, Inc.