Mathematics

Examples: Applying the ODE Initial Value Problem Solvers

This section contains several examples that illustrate the kinds of problems you can solve. For each example, there is a corresponding M-file, included in MATLAB. You can

• View the M-file code in an editor by entering edit followed by the name of the M-file at the MATLAB prompt. For example, to view the code for the simple nonstiff problem example, enter

• edit rigidode
  

• Alternatively, if you are reading this in the MATLAB Help Browser, you can click the name of the M-file in the list below.

• Run the example by entering the name of the M-file at the MATLAB prompt.

This section presents the following examples:

• Simple nonstiff problem (rigidode)
• Stiff problem (vdpode)
• Finite element discretization (fem1ode)
• Large, stiff, sparse problem (brussode)
• Simple event location (ballode)
• Advanced event location (orbitode)
• Differential-algebraic problem (hb1dae)
• Summary of Code Examples

Example: Simple Nonstiff Problem

rigidode illustrates the solution of a standard test problem proposed by Krogh for solvers intended for nonstiff problems [8].

The ODEs are the Euler equations of a rigid body without external forces.

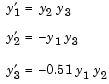
For your convenience, the entire problem is defined and solved in a single M-file. The differential equations are coded as a subfunction f. Because the example calls the ode45 solver without output arguments, the solver uses the default output function odeplot to plot the solution components.

To run this example, click on the example name, or type rigidode at the command line.

• function rigidode 
  %RIGIDODE  Euler equations of a rigid body without external forces
  tspan = [0 12];
  y0 = [0; 1; 1];
  
  % Solve the problem using ode45
  ode45(@f,tspan,y0);
  % ------------------------------------------------------------
  function dydt = f(t,y)
  dydt = [ y(2)*y(3) 
          -y(1)*y(3) 
          -0.51*y(1)*y(2) ];
  
  
  

Example: Stiff Problem (van der Pol Equation)

vdpode illustrates the solution of the van der Pol problem described in Example: The van der Pol Equation, µ = 1000 (Stiff). The differential equations

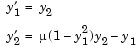
involve a constant parameter .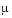

As 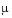increases, the problem becomes more stiff, and the period of oscillation becomes larger. When 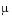is 1000 the equation is in relaxation oscillation and the problem is very stiff. The limit cycle has portions where the solution components change slowly and the problem is quite stiff, alternating with regions of very sharp change where it is not stiff (quasi-discontinuities).

By default, the solvers in the ODE suite that are intended for stiff problems approximate Jacobian matrices numerically. However, this example provides a nested function J(t,y) to evaluate the Jacobian matrix 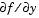analytically at (t,y) for 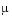= MU. The use of an analytic Jacobian can improve the reliability and efficiency of integration.

To run this example, click on the example name, or type vdpode at the command line. From the command line, you can specify a value of 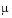as an argument to vdpode. The default is 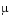= 1000.

• function vdpode(MU)
  %VDPODE  Parameterizable van der Pol equation (stiff for large MU)
  if nargin < 1
    MU = 1000;     % default
  end
  
  tspan = [0; max(20,3*MU)];              % Several periods
  y0 = [2; 0];
  options = odeset('Jacobian',@J);
  
  [t,y] = ode15s(@f,tspan,y0,options);
  
  plot(t,y(:,1));
  title(['Solution of van der Pol Equation, \mu = ' num2str(MU)]);
  xlabel('time t');
  ylabel('solution y_1');
  
  axis([tspan(1) tspan(end) -2.5 2.5]);  
  ---------------------------------------------------------------
  function dydt = f(t,y)
  dydt = [            y(2) 
           MU*(1-y(1)^2)*y(2)-y(1) ]; 
  end   % End nested function f
  ---------------------------------------------------------------
  function dfdy = J(t,y)
  dfdy = [         0                  1
           -2*MU*y(1)*y(2)-1    MU*(1-y(1)^2) ];
  end   % End nested function J
  end
  
  
  

Example: Finite Element Discretization

fem1ode illustrates the solution of ODEs that result from a finite element discretization of a partial differential equation. The value of N in the call fem1ode(N) controls the discretization, and the resulting system consists of N equations. By default, N is 19.

This example involves a mass matrix. The system of ODEs comes from a method of lines solution of the partial differential equation

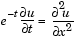
with initial condition 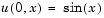and boundary conditions 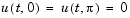. An integer 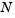is chosen, 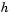is defined as 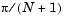, and the solution of the partial differential equation is approximated at 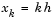for k = 0, 1, ..., N+1 by

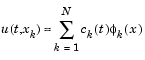
Here 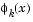is a piecewise linear function that is 1 at 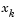and 0 at all the other 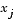. A Galerkin discretization leads to the system of ODEs

and the tridiagonal matrices 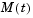and 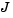are given by

and

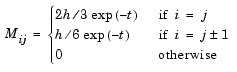
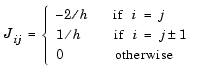
The initial values 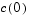are taken from the initial condition for the partial differential equation. The problem is solved on the time interval .

In the fem1ode example, the properties

• options = odeset('Mass',@mass,'MStateDep','none','Jacobian',J) 
  

indicate that the problem is of the form 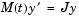. The nested function mass(t) evaluates the time-dependent mass matrix 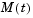and J is the constant Jacobian.

To run this example, click on the example name, or type fem1ode at the command line. From the command line, you can specify a value of 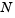as an argument to fem1ode. The default is 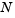= 19.

• function fem1ode(N)
  %FEM1ODE  Stiff problem with a time-dependent mass matrix 
  
  if nargin < 1
    N = 19;
  end
  h = pi/(N+1);
  y0 = sin(h*(1:N)');
  tspan = [0; pi];
  
  % The Jacobian is constant.
  e = repmat(1/h,N,1);    %  e=[(1/h) ... (1/h)];
  d = repmat(-2/h,N,1);   %  d=[(-2/h) ... (-2/h)]; 
  J = spdiags([e d e], -1:1, N, N);
  
  options = odeset('Mass',@mass,'MStateDependence','none', ...
                   'Jacobian',J);
  
  [t,y] = ode15s(@f,tspan,y0,options);
  
  surf((1:N)/(N+1),t,y);
  set(gca,'ZLim',[0 1]);
  view(142.5,30);
  title(['Finite element problem with time-dependent mass ' ...
         'matrix, solved by ODE15S']);
  xlabel('space ( x/\pi )');
  ylabel('time');
  zlabel('solution');
  %--------------------------------------------------------------
  -
  function out = f(t,y)
  h = pi/(N+1);
  e = repmat(1/h,N,1);    %  e=[(1/h) ... (1/h)];
  d = repmat(-2/h,N,1);   %  d=[(-2/h) ... (-2/h)]; 
  J = spdiags([e d e], -1:1, N, N);
  out = J*y;
  end   % End nested function f
  %--------------------------------------------------------------
  -
  function M = mass(t)
  h = pi/(N+1);
  e = repmat(exp(-t)*h/6,N,1);  % e(i)=exp(-t)*h/6
  e4 = repmat(4*exp(-t)*h/6,N,1); 
  M = spdiags([e e4 e], -1:1, N, N);
  end   % End nested function mass
  end
  
  
  

Example: Large, Stiff, Sparse Problem

brussode illustrates the solution of a (potentially) large stiff sparse problem. The problem is the classic "Brusselator" system [3] that models diffusion in a chemical reaction

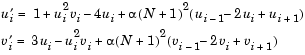
and is solved on the time interval [0,10] with 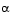= 1/50 and

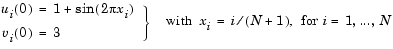
There are 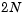equations in the system, but the Jacobian is banded with a constant width 5 if the equations are ordered as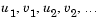

In the call brussode(N), where N corresponds to 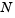, the parameter N 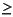2 specifies the number of grid points. The resulting system consists of 2N equations. By default, N is 20. The problem becomes increasingly stiff and the Jacobian increasingly sparse as N increases.

The nested function f(t,y) returns the derivatives vector for the Brusselator problem. The subfunction jpattern(N) returns a sparse matrix of 1s and 0s showing the locations of nonzeros in the Jacobian 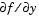. The example assigns this matrix to the property JPattern, and the solver uses the sparsity pattern to generate the Jacobian numerically as a sparse matrix. Providing a sparsity pattern can significantly reduce the number of function evaluations required to generate the Jacobian and can accelerate integration.

For the Brusselator problem, if the sparsity pattern is not supplied, 2N evaluations of the function are needed to compute the 2N-by-2N Jacobian matrix. If the sparsity pattern is supplied, only four evaluations are needed, regardless of the value of N.

To run this example, click on the example name, or type brussode at the command line. From the command line, you can specify a value of 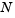as an argument to brussode. The default is 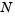 = 20.

• function brussode(N)
  %BRUSSODE  Stiff problem modeling a chemical reaction 
  
  if nargin < 1
    N = 20;
  end
  
  tspan = [0; 10];
  y0 = [1+sin((2*pi/(N+1))*(1:N));
  repmat(3,1,N)];
  
  options = odeset('Vectorized','on','JPattern',jpattern(N));
  
  [t,y] = ode15s(@f,tspan,y0,options);
  
  u = y(:,1:2:end);
  x = (1:N)/(N+1);
  surf(x,t,u);
  view(-40,30);
  xlabel('space');
  ylabel('time');
  zlabel('solution u');
  title(['The Brusselator for N = ' num2str(N)]);
  % --------------------------------------------------------------
  function dydt = f(t,y)
  c = 0.02 * (N+1)^2;
  dydt = zeros(2*N,size(y,2));      % preallocate dy/dt
  % Evaluate the two components of the function at one edge of 
  % the grid (with edge conditions).
  i = 1;
  dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ...
              c*(1-2*y(i,:)+y(i+2,:));
  dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ...
                c*(3-2*y(i+1,:)+y(i+3,:));
  % Evaluate the two components of the function at all interior 
  % grid points.
  i = 3:2:2*N-3;
  dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ...
              c*(y(i-2,:)-2*y(i,:)+y(i+2,:));
  dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ...
                c*(y(i-1,:)-2*y(i+1,:)+y(i+3,:));
  % Evaluate the two components of the function at the other edge 
  % of the grid (with edge conditions).
  i = 2*N-1;
  dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ...
              c*(y(i-2,:)-2*y(i,:)+1);
  dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ...
                c*(y(i-1,:)-2*y(i+1,:)+3);
  end   % End nested function f
  end   % End function brussode
  % --------------------------------------------------------------
  function S = jpattern(N)
  B = ones(2*N,5);
  B(2:2:2*N,2) = zeros(N,1);
  B(1:2:2*N-1,4) = zeros(N,1);
  S = spdiags(B,-2:2,2*N,2*N);
  end;
  
  
  

Example: Simple Event Location

ballode models the motion of a bouncing ball. This example illustrates the event location capabilities of the ODE solvers.

The equations for the bouncing ball are

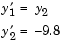
In this example, the event function is coded in a subfunction events

• [value,isterminal,direction] = events(t,y)
  

which returns

• A value of the event function
• The information whether or not the integration should stop when value = 0 (isterminal = 1 or 0, respectively)
• The desired directionality of the zero crossings:

-1	Detect zero crossings in the negative direction only
0	Detect all zero crossings
1	Detect zero crossings in the positive direction only

The length of value, isterminal, and direction is the same as the number of event functions. The ith element of each vector, corresponds to the ith event function. For an example of more advanced event location, see orbitode (Example: Advanced Event Location).

In ballode, setting the Events property to @events causes the solver to stop the integration (isterminal = 1) when the ball hits the ground (the height y(1) is 0) during its fall (direction = -1). The example then restarts the integration with initial conditions corresponding to a ball that bounced.

To run this example, click on the example name, or type ballode at the command line.

• function ballode
  %BALLODE  Run a demo of a bouncing ball.
  
  tstart = 0;
  tfinal = 30;
  y0 = [0; 20];
  refine = 4;
  options = odeset('Events',@events,'OutputFcn', @odeplot,...
                   'OutputSel',1,'Refine',refine);
  
  set(gca,'xlim',[0 30],'ylim',[0 25]);
  box on
  hold on;
  
  tout = tstart;
  yout = y0.';
  teout = [];
  yeout = [];
  ieout = [];
  for i = 1:10
    % Solve until the first terminal event.
    [t,y,te,ye,ie] = ode23(@f,[tstart tfinal],y0,options);
    if ~ishold
      hold on
    end
    % Accumulate output.  
    nt = length(t);
    tout = [tout; t(2:nt)];
    yout = [yout; y(2:nt,:)];
    teout = [teout; te];    % Events at tstart are never reported.
    yeout = [yeout; ye];
    ieout = [ieout; ie];
  
    ud = get(gcf,'UserData');
    if ud.stop
      break;
    end
    
    % Set the new initial conditions, with .9 attenuation.
    y0(1) = 0;
    y0(2) = -.9*y(nt,2);
  
    % A good guess of a valid first time step is the length of 
    % the last valid time step, so use it for faster computation.
    options = odeset(options,'InitialStep',t(nt)-t(nt-refine),...
                             'MaxStep',t(nt)-t(1));
    tstart = t(nt);
  end
  
  plot(teout,yeout(:,1),'ro')
  xlabel('time');
  ylabel('height');
  title('Ball trajectory and the events');
  hold off
  odeplot([],[],'done');
  % --------------------------------------------------------------
  function dydt = f(t,y)
  dydt = [y(2); -9.8];
  % --------------------------------------------------------------
  function [value,isterminal,direction] = events(t,y)
  % Locate the time when height passes through zero in a 
  % decreasing direction and stop integration.
  value = y(1);     % Detect height = 0
  isterminal = 1;   % Stop the integration
  direction = -1;   % Negative direction only
  
  
  

Example: Advanced Event Location

orbitode illustrates the solution of a standard test problem for those solvers that are intended for nonstiff problems. It traces the path of a spaceship traveling around the moon and returning to the earth. (Shampine and Gordon [8], p.246).

The orbitode problem is a system of the following four equations shown:

where

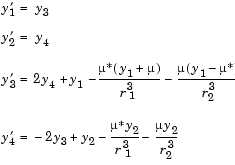
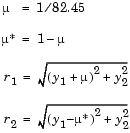
The first two solution components are coordinates of the body of infinitesimal mass, so plotting one against the other gives the orbit of the body. The initial conditions have been chosen to make the orbit periodic. The value of corresponds to a spaceship traveling around the moon and the earth. Moderately stringent tolerances are necessary to reproduce the qualitative behavior of the orbit. Suitable values are 1e-5 for RelTol and 1e-4 for AbsTol.

The nested events function includes event functions that locate the point of maximum distance from the starting point and the time the spaceship returns to the starting point. Note that the events are located accurately, even though the step sizes used by the integrator are not determined by the location of the events. In this example, the ability to specify the direction of the zero crossing is critical. Both the point of return to the initial point and the point of maximum distance have the same event function value, and the direction of the crossing is used to distinguish them.

To run this example, click on the example name, or type orbitode at the command line. The example uses the output function odephas2 to produce the two-dimensional phase plane plot and let you to see the progress of the integration.

• function orbitode
  %ORBITODE  Restricted three-body problem
  
  mu = 1 / 82.45;
  mustar = 1 - mu;
  y0 = [1.2; 0; 0; -1.04935750983031990726];
  tspan = [0 7];
  
  options = odeset('RelTol',1e-5,'AbsTol',1e-4,...
                   'OutputFcn',@odephas2,'Events',@events);
  
  [t,y,te,ye,ie] = ode45(@f,tspan,y0,options);
  
  plot(y(:,1),y(:,2),ye(:,1),ye(:,2),'o');
  title ('Restricted three body problem')
  ylabel ('y(t)')
  xlabel ('x(t)')
  % --------------------------------------------------------------
  function dydt = f(t,y)
  r13 = ((y(1) + mu)^2 + y(2)^2) ^ 1.5;
  r23 = ((y(1) - mustar)^2 + y(2)^2) ^ 1.5;
  dydt = [ y(3)
           y(4)
           2*y(4) + y(1) - mustar*((y(1)+mu)/r13) - ...
                           mu*((y(1)-mustar)/r23)
          -2*y(3) + y(2) - mustar*(y(2)/r13) - mu*(y(2)/r23) ];
  end   % End nested function f
  % --------------------------------------------------------------
  function [value,isterminal,direction] = events(t,y)
  % Locate the time when the object returns closest to the 
  % initial point y0 and starts to move away, and stop integration.
  % Also locate the time when the object is farthest from the 
  % initial point y0 and starts to move closer.
  % 
  % The current distance of the body is
  % 
  %   DSQ = (y(1)-y0(1))^2 + (y(2)-y0(2))^2 
  %       = <y(1:2)-y0(1:2),y(1:2)-y0(1:2)>
  % 
  % A local minimum of DSQ occurs when d/dt DSQ crosses zero 
  % heading in the positive direction.  We can compute d(DSQ)/dt as
  % 
  %  d(DSQ)/dt = 2*(y(1:2)-y0(1:2))'*dy(1:2)/dt = ... 
  %                 2*(y(1:2)-y0(1:2))'*y(3:4)
  % 
  dDSQdt = 2 * ((y(1:2)-y0(1:2))' * y(3:4));
  value = [dDSQdt; dDSQdt];
  isterminal = [1; 0];            % Stop at local minimum
  direction = [1; -1];            % [local minimum, local maximum]
  end   % End nested function events
  end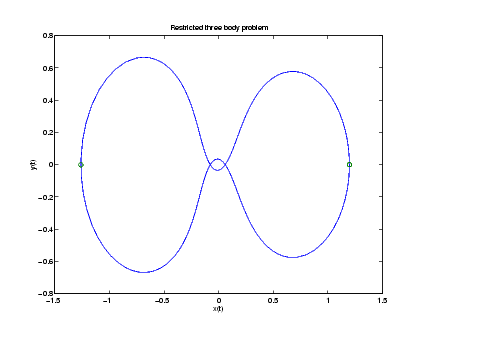 
  

Example: Differential-Algebraic Problem

hb1dae reformulates the hb1ode example as a differential-algebraic equation (DAE) problem. The Robertson problem coded in hb1ode is a classic test problem for codes that solve stiff ODEs.

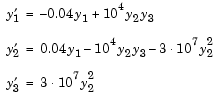
Note    The Robertson problem appears as an example in the prolog to LSODI [4].

In hb1ode, the problem is solved with initial conditions 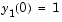, , 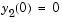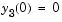to steady state. These differential equations satisfy a linear conservation law that is used to reformulate the problem as the DAE

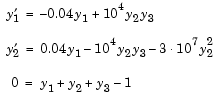
Obviously these equations do not have a solution for 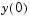with components that do not sum to 1. The problem has the form of 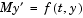with

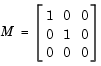
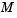is obviously singular, but hb1dae does not inform the solver of this. The solver must recognize that the problem is a DAE, not an ODE. Similarly, although consistent initial conditions are obvious, the example uses an inconsistent value 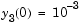to illustrate computation of consistent initial conditions.

To run this example, click on the example name, or type hb1dae at the command line. Note that hb1dae:

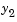• Imposes a much smaller absolute error tolerance on than on the other components. This is because 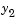is much smaller than the other components and its major change takes place in a relatively short time.
• Specifies additional points at which the solution is computed to more clearly show the behavior of .
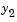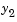• Multiplies by 10⁴ to make 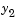visible when plotting it with the rest of the solution.
• Uses a logarithmic scale to plot the solution on the long time interval.

• function hb1dae
  %HB1DAE  Stiff differential-algebraic equation (DAE)
  
  % A constant, singular mass matrix
  M = [1 0 0
       0 1 0 
       0 0 0];
  
  % Use an inconsistent initial condition to test initialization.
  y0 = [1; 0; 1e-3];
  tspan = [0 4*logspace(-6,6)];
  
  % Use the LSODI example tolerances. The 'MassSingular' property
  % is left at its default 'maybe' to test the automatic detection
  % of a DAE.
  options = odeset('Mass',M,'RelTol',1e-4,...
                   'AbsTol',[1e-6 1e-10 1e-6],'Vectorized','on');
  
  [t,y] = ode15s(@f,tspan,y0,options);
  
  y(:,2) = 1e4*y(:,2);
  
  semilogx(t,y);
  ylabel('1e4 * y(:,2)');
  title(['Robertson DAE problem with a Conservation Law, '...
         'solved by ODE15S']);
  xlabel('This is equivalent to the stiff ODEs coded in HB1ODE.');
  % --------------------------------------------------------------
  function out = f(t,y)
  out = [ -0.04*y(1,:) + 1e4*y(2,:).*y(3,:)
           0.04*y(1,:) - 1e4*y(2,:).*y(3,:) - 3e7*y(2,:).^2
           y(1,:) + y(2,:) + y(3,:) - 1 ];
  
  
  

Summary of Code Examples

The following table lists the M-files for all the ODE initial value problem examples. Click the example name to see the code in an editor. Type the example name at the command line to run it.

Note    The Differential Equations Examples browser enables you to view the code for the ODE examples and DAE examples. You can also run the examples from the browser. Click on these links to invoke the browser, or type odeexamples('ode')or odeexamples('dae')at the command line.

Example	Description
amp1dae	Stiff DAE -- electrical circuit
ballode	Simple event location -- bouncing ball
batonode	ODE with time- and state-dependent mass matrix -- motion of a baton
brussode	Stiff large problem -- diffusion in a chemical reaction (the Brusselator)
burgersode	ODE with strongly state-dependent mass matrix -- Burger's equation solved using a moving mesh technique
fem1ode	Stiff problem with a time-dependent mass matrix -- finite element method
fem2ode	Stiff problem with a constant mass matrix -- finite element method
hb1ode	Stiff ODE problem solved on a very long interval -- Robertson chemical reaction
hb1dae	Robertson problem -- stiff, linearly implicit DAE from a conservation law
ihb1dae	Robertson problem -- stiff, fully implicit DAE
iburgersode	Burgers' equation solved as implicit ODE system
orbitode	Advanced event location -- restricted three body problem
rigidode	Nonstiff problem -- Euler equations of a rigid body without external forces
vdpode	Parameterizable van der Pol equation (stiff for large )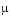

Changing ODE Integration Properties

Questions and Answers, and Troubleshooting

© 1994-2005 The MathWorks, Inc.