bvpinit (MATLAB Functions)

Form the initial guess for bvp4c

Syntax

solinit = bvpinit(x,yinit)
solinit = bvpinit(x,yinit,parameters)
solinit = bvpinit(sol,[anew bnew])
solinit = bvpinit(sol,[anew bnew],parameters)

Description

solinit = bvpinit(x,yinit) forms the initial guess for the boundary value problem solver bvp4c.

x is a vector that specifies an initial mesh. If you want to solve the boundary value problem (BVP) on 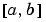, then specify x(1) as 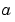and x(end) as 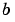. The function bvp4c adapts this mesh to the solution, so a guess like x = linspace(a,b,10) often suffices. However, in difficult cases, you should place mesh points where the solution changes rapidly. The entries of x must be in

Increasing order if
Decreasing order if

For two-point boundary value problems, the entries of x must be distinct. That is, if 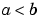, the entries must satisfy x(1) < x(2) < ... < x(end). If 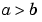, the entries must satisfy x(1) > x(2) > ... > x(end)

For multipoint boundary value problem, you can specify the points in 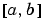at which the boundary conditions apply, other than the endpoints a and b, by repeating their entries in x. For example, if you set

```
x = [0, 0.5, 1, 1,  1.5, 2];
```

the boundary conditions apply at three points: the endpoints 0 and 2, and the repeated entry 1. In general, repeated entries represent boundary points between regions in 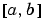. In the preceding example, the repeated entry 1 divides the interval [0,2] into two regions: [0,1] and [1,2].

yinit is a guess for the solution. It can be either a vector, or a function:

Vector - For each component of the solution, bvpinit replicates the corresponding element of the vector as a constant guess across all mesh points. That is, yinit(i) is a constant guess for the ith component yinit(i,:) of the solution at all the mesh points in x.
Function - For a given mesh point, the guess function must return a vector whose elements are guesses for the corresponding components of the solution. The function must be of the form

```
y = guess(x)
```

where x is a mesh point and y is a vector whose length is the same as the number of components in the solution. For example, if the guess function is an M-file function, bvpinit calls
- ```
y(:,j) = guess(x(j))
```
at each mesh point.

For multipoint boundary value problems, the guess function must be of the form
- ```
y = guess(x, k)
```
where y an initial guess for the solution at x in region k. The function must accept the input argument k, which is provided for flexibility in writing the guess function. However, the function is not required to use k.

solinit = bvpinit(x,yinit,parameters) indicates that the boundary value problem involves unknown parameters. Use the vector parameters to provide a guess for all unknown parameters.

solinit is a structure with the following fields. The structure can have any name, but the fields must be named x, y, and parameters.

x
Ordered nodes of the initial mesh.

y
Initial guess for the solution with solinit.y(:,i) a guess for the solution at the node solinit.x(i).

parameters
Optional. A vector that provides an initial guess for unknown parameters.

`x`	Ordered nodes of the initial mesh.
`y`	Initial guess for the solution with `solinit.y(:,i)` a guess for the solution at the node `solinit.x(i)`.
`parameters`	Optional. `A` vector that provides an initial guess for unknown parameters.

solinit = bvpinit(sol,[anew bnew]) forms an initial guess on the interval [anew bnew] from a solution sol on an interval 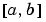. The new interval must be larger than the previous one, so either anew <= a < b <= bnew or anew >= a > b >= bnew. The solution sol is extrapolated to the new interval. If sol contains parameters, they are copied to solinit.

solinit = bvpinit(sol,[anew bnew],parameters) forms solinit as described above, but uses parameters as a guess for unknown parameters in solinit.

See Also

@ (function_handle), bvp4c, bvpget, bvpset, deval

bvpget bvpset