

| MATLAB Function Reference |   |
Solve boundary value problems (BVPs) for ordinary differential equations
Syntax
Arguments
odefun |
A function handle that evaluates the differential equations 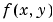 . It can have the form . It can have the formwhere x is a scalar corresponding to 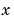 , and , and y is a column vector corresponding to 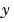 . . parameters is a vector of unknown parameters. The output dydx is a column vector. | |
bcfun |
A function handle that computes the residual in the boundary conditions. For two-point boundary value conditions of the form 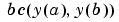 , , bcfun can have the formwhere ya and yb are column vectors corresponding to 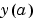 and and 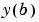 . . parameters is a vector of unknown parameters. The output res is a column vector.See Multipoint Boundary Value Problems for a description of bcfun for multipoint boundary value problems. | |
solinit |
A structure containing the initial guess for a solution. You create solinit using the function bvpinit. solinit has the following fields. | |
|
x |
Ordered nodes of the initial mesh. Boundary conditions are imposed at 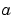 = = solinit.x(1) and 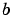 = = solinit.x(end). |
|
y |
Initial guess for the solution such that solinit.y(:,i) is a guess for the solution at the node solinit.x(i). |
|
parameters |
Optional. A vector that provides an initial guess for unknown parameters. |
|
The structure can have any name, but the fields must be named x, y, and parameters. You can form solinit with the helper function bvpinit. See bvpinit for details. | |
options |
Optional integration argument. A structure you create using the bvpset function. See bvpset for details. | |
Description
sol = bvp4c(odefun,bcfun,solinit)
integrates a system of ordinary differential equations of the form
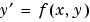
on the interval [a,b] subject to two-point boundary value conditions
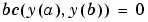
odefun and bcfun are function handles. See Function Handles in the MATLAB Programming documentation for more information.
Parameterizing Functions Called by Function Functions, in the MATLAB mathematics documentation, explains how to provide additional parameters to the function odefun, as well as the boundary condition function bcfun, if necessary.
bvp4c can also solve multipoint boundary value problems. See Multipoint Boundary Value Problems. You can use the function bvpinit to specify the boundary points, which are stored in the input argument solinit. See the reference page for bvpint for more information.
The bvp4c solver can also find unknown parameters 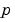 for problems of the form
for problems of the form
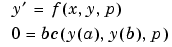
where 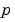 corresponds to
corresponds to parameters. You provide bvp4c an initial guess for any unknown parameters in solinit.parameters. The bvp4c solver returns the final values of these unknown parameters in sol.parameters.
bvp4c produces a solution that is continuous on [a,b] and has a continuous first derivative there. Use the function deval and the output sol of bvp4c to evaluate the solution at specific points xint in the interval [a,b].
The structure sol returned by bvp4c has the following fields:
The structure sol can have any name, and bvp4c creates the fields x, y, yp, parameters, and solver.
sol = bvp4c(odefun,bcfun,solinit,options)
solves as above with default integration properties replaced by the values in options, a structure created with the bvpset function. See bvpset for details.
solinit = bvpinit(x, yinit, params) forms the initial guess solinit with the vector params of guesses for the unknown parameters.
Singular Boundary Value Problems
bvp4c solves a class of singular boundary value problems, including problems with unknown parameters p, of the form
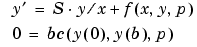
The interval is required to be [0, b] with b > 0. Often such problems arise when computing a smooth solution of ODEs that result from partial differential equations (PDEs) due to cylindrical or spherical symmetry. For singular problems, you specify the (constant) matrix S as the value of the 'SingularTerm' option of bvpset, and odefun evaluates only f(x, y, p). The boundary conditions must be consistent with the necessary condition 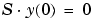 and the initial guess should satisfy this condition.
and the initial guess should satisfy this condition.
Multipoint Boundary Value Problems
bvp4c can solve multipoint boundary value problems where
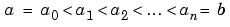 are boundary points in the interval
are boundary points in the interval 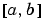 . The points
. The points 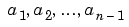 represent interfaces that divide
represent interfaces that divide 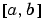 into regions.
into regions. bvp4c enumerates the regions from left to right (from a to b), with indices starting from 1. In region k, 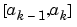 ,
, bvp4c evaluates the derivative as
In the boundary conditions function
yleft(:, k) is the solution at the left boundary of 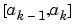 . Similarly,
. Similarly, yright(:, k) is the solution at the right boundary of region k. In particular,
For example, if there just one equation and the boundary points are 0 < 1 < 2, to specify the boundary conditions
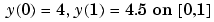
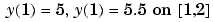
yleft and yright have the following values.
The boundary condition function bcfun has the form
function res = bc(yleft, yright) res = [ yleft(1) - 4 yright(1) - 4.5 yleft(2) - 5 yright(2) - 5.5];
When you create an initial guess with
use double entries in xinit for each interface point. See the reference page for bvpinit for more information.
If yinit is a function, bvpinit calls y = yinit(x, k) to get an initial guess for the solution at x in region k. In the solution structure sol returned by bpv4c, sol.x has double entries for each interface point. The corresponding columns of sol.y contain the left and right solution at the interface, respectively.
For an example of solving a three-point boundary value problem, enter
Examples
Example 1. Boundary value problems can have multiple solutions and one purpose of the initial guess is to indicate which solution you want. The second order differential equation
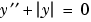
has exactly two solutions that satisfy the boundary conditions
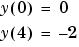
Prior to solving this problem with bvp4c, you must write the differential equation as a system of two first order ODEs
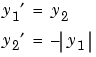
Here 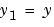 and
and 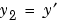 . This system has the required form
. This system has the required form
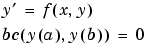
The function 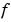 and the boundary conditions
and the boundary conditions 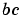 are coded in MATLAB as functions
are coded in MATLAB as functions twoode and twobc.
function dydx = twoode(x,y) dydx = [ y(2) -abs(y(1))]; function res = twobc(ya,yb) res = [ ya(1) yb(1) + 2];
Form a guess structure consisting of an initial mesh of five equally spaced points in [0,4] and a guess of constant values 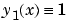 and
and 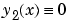 with the command
with the command
Evaluate the numerical solution at 100 equally spaced points and plot 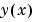 with
with
You can obtain the other solution of this problem with the initial guess
Example 2. This boundary value problem involves an unknown parameter. The task is to compute the fourth (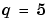 ) eigenvalue
) eigenvalue 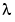 of Mathieu's equation
of Mathieu's equation
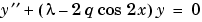
Because the unknown parameter 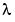 is present, this second order differential equation is subject to three boundary conditions
is present, this second order differential equation is subject to three boundary conditions
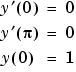
It is convenient to use subfunctions to place all the functions required by bvp4c in a single M-file.
function mat4bvp lambda = 15; solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda); sol = bvp4c(@mat4ode,@mat4bc,solinit); fprintf('The fourth eigenvalue is approximately %7.3f.\n',... sol.parameters) xint = linspace(0,pi); Sxint = deval(sol,xint); plot(xint,Sxint(1,:)) axis([0 pi -1 1.1]) title('Eigenfunction of Mathieu''s equation.') xlabel('x') ylabel('solution y') % ------------------------------------------------------------ function dydx = mat4ode(x,y,lambda) q = 5; dydx = [ y(2) -(lambda - 2*q*cos(2*x))*y(1) ]; % ------------------------------------------------------------ function res = mat4bc(ya,yb,lambda) res = [ ya(2) yb(2) ya(1)-1 ]; % ------------------------------------------------------------ function yinit = mat4init(x) yinit = [ cos(4*x) -4*sin(4*x) ];
The differential equation (converted to a first order system) and the boundary conditions are coded as subfunctions mat4ode and mat4bc, respectively. Because unknown parameters are present, these functions must accept three input arguments, even though some of the arguments are not used.
The guess structure solinit is formed with bvpinit. An initial guess for the solution is supplied in the form of a function mat4init. We chose 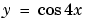 because it satisfies the boundary conditions and has the correct qualitative behavior (the correct number of sign changes). In the call to
because it satisfies the boundary conditions and has the correct qualitative behavior (the correct number of sign changes). In the call to bvpinit, the third argument (lambda = 15) provides an initial guess for the unknown parameter 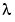 .
.
After the problem is solved with bvp4c, the field sol.parameters returns the value 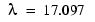 , and the plot shows the eigenfunction associated with this eigenvalue.
, and the plot shows the eigenfunction associated with this eigenvalue.
Algorithms
bvp4c is a finite difference code that implements the three-stage Lobatto IIIa formula. This is a collocation formula and the collocation polynomial provides a C1-continuous solution that is fourth order accurate uniformly in [a,b]. Mesh selection and error control are based on the residual of the continuous solution.
See Also
function_handle (@), bvpget, bvpinit, bvpset, deval
References
[1] Shampine, L.F., M.W. Reichelt, and J. Kierzenka, "Solving Boundary Value
Problems for Ordinary Differential Equations in MATLAB with bvp4c,"
available at www.mathworks.com/bvp_tutorial.
 | builtin | bvpget |  |
© 1994-2005 The MathWorks, Inc.