

| MATLAB Function Reference |   |
Create or alter boundary value problem (BVP) options structure
Syntax
options = bvpset('name1',value1,'name2',value2,...) options = bvpset(oldopts'name1',value1,...) options = bvpset(oldopts,newopts) bvpset
Description
options = bvpset('name1',value1,'name2',value2,...)
creates a structure options that you can supply to the boundary value problem solver bvp4c, in which the named properties have the specified values. Any unspecified properties retain their default values. For all properties, it is sufficient to type only the leading characters that uniquely identify the property. bvpset ignores case for property names.
options = bvpset(oldopts,'name1',value1,...)
alters an existing options structure oldopts. This overwrites any values in oldopts that are specified using name/value pairs and returns the modified structure as the output argument.
options = bvpset(oldopts,newopts)
combines an existing options structure oldopts with a new options structure newopts. Any values set in newopts overwrite the corresponding values in oldopts.
bvpset
with no input arguments displays all property names and their possible values, indicating defaults with braces {}.
You can use the function bvpget to query the options structure for the value of a specific property.
BVP Properties
bvpset enables you to specify properties for the boundary value problem solver bvp4c. There are several categories of properties that you can set:
Error Tolerance Properties
Because bvp4c uses a collocation formula, the numerical solution is based on a mesh of points at which the collocation equations are satisfied. Mesh selection and error control are based on the residual of this solution, such that the computed solution 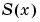 is the exact solution of a perturbed problem
is the exact solution of a perturbed problem 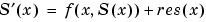 . On each subinterval of the mesh, a norm of the residual in the
. On each subinterval of the mesh, a norm of the residual in the ith component of the solution, res(i), is estimated and is required to be less than or equal to a tolerance. This tolerance is a function of the relative and absolute tolerances, RelTol and AbsTol, defined by the user.
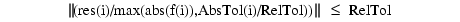
The following table describes the error tolerance properties.
Vectorization
The following table describes the BVP vectorization property. Vectorization of the ODE function used by bvp4c differs from the vectorization used by the ODE solvers:
bvp4c, the ODE function must be vectorized with respect to the first argument as well as the second one, so that F([x1 x2 ...],[y1 y2 ...]) returns [F(x1,y1) F(x2,y2) ...].
bvp4c benefits from vectorization even when analytical Jacobians are provided. For stiff ODE solvers, vectorization is ignored when analytical Jacobians are used.| Property |
Value |
Description |
Vectorized |
on | {off} |
Set on to inform bvp4c that you have coded the ODE function F so that F([x1 x2 ...],[y1 y2 ...]) returns [F(x1,y1) F(x2,y2) ...]. That is, your ODE function can pass to the solver a whole array of column vectors at once. This enables the solver to reduce the number of function evaluations and may significantly reduce solution time.With the MATLAB array notation, it is typically an easy matter to vectorize an ODE function. In the shockbvp example shown previously, the shockODE function has been vectorized using colon notation into the subscripts and by using the array multiplication (.*) operator. |
Analytical Partial Derivatives
By default, the bvp4c solver approximates all partial derivatives with finite differences. bvp4c can be more efficient if you provide analytical partial derivatives 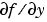 of the differential equations, and analytical partial derivatives,
of the differential equations, and analytical partial derivatives, 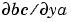 and
and 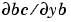 , of the boundary conditions. If the problem involves unknown parameters, you must also provide partial derivatives,
, of the boundary conditions. If the problem involves unknown parameters, you must also provide partial derivatives, 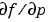 and
and 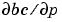 , with respect to the parameters.
, with respect to the parameters.
The following table describes the analytical partial derivatives properties.
| Property |
Value |
Description |
FJacobian |
Function handle |
Handle to a function that computes the analytical partial derivatives of 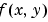 . When solving . When solving 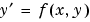 , set this property to , set this property to @fjac if dfdy = fjac(x,y) evaluates the Jacobian 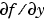 . If the problem involves unknown parameters . If the problem involves unknown parameters 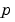 , , [dfdy,dfdp] = fjac(x,y,p) must also return the partial derivative 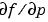 . For problems with constant partial derivatives, set this property to the value of . For problems with constant partial derivatives, set this property to the value of dfdy or to a cell array {dfdy,dfdp}.See Function Handles in the MATLAB Programming documentation for more information. |
BCJacobian |
Function handle |
Handle to a function that computes the analytical partial derivatives of 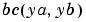 . For boundary conditions . For boundary conditions 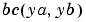 , set this property to , set this property to @bcjac if [dbcdya,dbcdyb] = bcjac(ya,yb) evaluates the partial derivatives 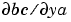 , and , and 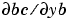 . If the problem involves unknown parameters . If the problem involves unknown parameters 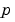 , , [dbcdya,dbcdyb,dbcdp] = bcjac(ya,yb,p) must also return the partial derivative 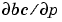 . For problems with constant partial derivatives, set this property to a cell array . For problems with constant partial derivatives, set this property to a cell array {dbcdya,dbcdyb} or {dbcdya,dbcdyb,dbcdp}. |
Singular BVPs
bvp4c can solve singular problems of the form
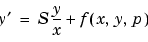
posed on the interval 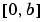 where
where 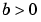 . For such problems, specify the constant matrix
. For such problems, specify the constant matrix 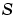 as the value of
as the value of SingularTerm. For equations of this form, odefun evaluates only the 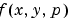 term, where
term, where 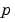 represents unknown parameters, if any.
represents unknown parameters, if any.
| Property |
Value |
Description |
SingularTerm |
Constant matrix |
Singular term of singular BVPs. Set to the constant matrix 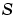 for equations of the form for equations of the form posed on the interval 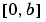 where where 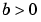 . . |
Mesh Size Property
bvp4c solves a system of algebraic equations to determine the numerical solution to a BVP at each of the mesh points. The size of the algebraic system depends on the number of differential equations (n) and the number of mesh points in the current mesh (N). When the allowed number of mesh points is exhausted, the computation stops, bvp4c displays a warning message and returns the solution it found so far. This solution does not satisfy the error tolerance, but it may provide an excellent initial guess for computations restarted with relaxed error tolerances or an increased value of NMax.
The following table describes the mesh size property.
Solution Statistic Property
The Stats property lets you view solution statistics.
The following table describes the solution statistics property.
| Property |
Value |
Description |
Stats |
on | {off} |
Specifies whether statistics about the computations are displayed. If the |
Example
To create an options structure that changes the relative error tolerance of bvp4c from the default value of 1e-3 to 1e-4, enter
To recover the value of 'RelTol' from options, enter
See Also
@ (function_handle), bvp4c, bvpget, bvpinit, deval
 | bvpinit | bvpval |  |
© 1994-2005 The MathWorks, Inc.