Image Processing Toolbox User's Guide

Transforms

The usual mathematical representation of an image is a function of two spatial variables:

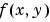. The value of the function at a particular location

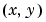represents the intensity of the image at that point. This is called the spatial domain. The term transform refers to an alternative mathematical representation of an image. For example, the Fourier transform is a representation of an image as a sum of complex exponentials of varying magnitudes, frequencies, and phases. This is called the frequency domain. Transforms are useful for a wide range of purposes, including convolution, enhancement, feature detection, and compression.
This chapter defines several important transforms and shows examples of their application to image processing.

Fourier Transform	Defines the Fourier transform and some of its applications in image processing
Discrete Cosine Transform	Describes the discrete cosine transform (DCT) of an image and its application, particularly in image compression
Radon Transform	Describes how the Image Processing Toolbox `radon` function computes projections of an image matrix along specified directions
Fan-Beam Projection Data	Describes how the Image Processing Toolbox `radon` function computes projections of an image matrix along specified directions

Computing the Frequency Response of a Filter Fourier Transform