prony (Signal Processing Toolbox)

Prony's method for time domain IIR filter design

Syntax

```
[b,a] = prony(h,n,m)
```

Description

Prony's method is an algorithm for finding an IIR filter with a prescribed time domain impulse response. It has applications in filter design, exponential signal modeling, and system identification (parametric modeling).

[b,a] = prony(h,n,m) finds a filter with numerator order n, denominator order m, and the time domain impulse response in h. If the length of h is less than the largest order (n or m), h is padded with zeros. prony returns the filter coefficients in row vectors b and a, of length n + 1 and m + 1, respectively. The filter coefficients are in descending powers of z.

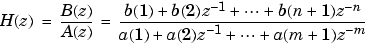
Examples

Recover the coefficients of a Butterworth filter from its impulse response:

[b,a] = butter(4,0.2)
b = 
    0.0048    0.0193    0.0289    0.0193    0.0048
a =
    1.0000    -2.3695    2.3140    -1.0547    0.1874
h = filter(b,a,[1 zeros(1,25)]);
[bb,aa] = prony(h,4,4)
bb = 
    0.0048    0.0193    0.0289    0.0193    0.0048
ab =
    1.0000    -2.3695    2.3140    -1.0547    0.1874

Algorithm

prony implements the method described in reference [1]. This method uses a variation of the covariance method of AR modeling to find the denominator coefficients a and then finds the numerator coefficients b for which the impulse response of the output filter matches exactly the first n + 1 samples of x. The filter is not necessarily stable, but potentially can recover the coefficients exactly if the data sequence is truly an autoregressive moving-average (ARMA) process of the correct order.

See Also

butter, cheby1, cheby2, ellip, invfreqz, levinson, lpc, stmcb

References

[1] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, 1987, pp. 226-228.

polystab pulstran