invfreqz (Signal Processing Toolbox)

Identify discrete-time filter parameters from frequency response data

Syntax

[b,a] = invfreqz(h,w,n,m)
[b,a] = invfreqz(h,w,n,m,wt)
[b,a] = invfreqz(h,w,n,m,wt,iter)
[b,a] = invfreqz(h,w,n,m,wt,iter,tol)
[b,a] = invfreqz(h,w,n,m,wt,iter,tol,'trace')
[b,a] = invfreqz(h,w,'complex',n,m,...)

Description

invfreqz is the inverse operation of freqz; it finds a discrete-time transfer function that corresponds to a given complex frequency response. From a laboratory analysis standpoint, invfreqz can be used to convert magnitude and phase data into transfer functions.

[b,a] = invfreqz(h,w,n,m) returns the real numerator and denominator coefficients in vectors b and a of the transfer function

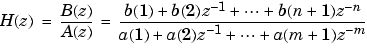
whose complex frequency response is given in vector h at the frequency points specified in vector w. Scalars n and m specify the desired orders of the numerator and denominator polynomials.

Frequency is specified in radians between 0 and 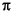, and the length of h must be the same as the length of w. invfreqz uses conj(h) at -w to ensure the proper frequency domain symmetry for a real filter.

[b,a] = invfreqz(h,w,n,m,wt) weights the fit-errors versus frequency, where wt is a vector of weighting factors the same length as w.

[b,a] = invfreqz(h,w,n,m,wt,iter) and

[b,a] = invfreqz(h,w,n,m,wt,iter,tol) provide a superior algorithm that guarantees stability of the resulting linear system and searches for the best fit using a numerical, iterative scheme. The iter parameter tells invfreqz to end the iteration when the solution has converged, or after iter iterations, whichever comes first. invfreqz defines convergence as occurring when the norm of the (modified) gradient vector is less than tol, where tol is an optional parameter that defaults to 0.01. To obtain a weight vector of all ones, use

```
invfreqz(h,w,n,m,[],iter,tol)
```

[b,a] = invfreqz(h,w,n,m,wt,iter,tol,'trace') displays a textual progress report of the iteration.

[b,a] = invfreqz(h,w,'complex',n,m,...) creates a complex filter. In this case no symmetry is enforced, and the frequency is specified in radians between 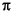- and .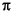

Examples

Convert a simple transfer function to frequency response data and then back to the original filter coefficients:

a = [1 2 3 2 1 4]; b = [1 2 3 2 3];
[h,w] = freqz(b,a,64);
[bb,aa] = invfreqz(h,w,4,5)
bb =
    1.0000    2.0000    3.0000    2.0000    3.0000
aa =
    1.0000    2.0000    3.0000    2.0000    1.0000    4.0000

Notice that bb and aa are equivalent to b and a, respectively. However, aa has poles outside the unit circle and thus the system is unstable. Use invfreqz's iterative algorithm to find a stable approximation to the system:

[bbb,aaa] = invfreqz(h,w,4,5,[],30)
bbb =
    0.2427    0.2788    0.0069    0.0971    0.1980
aaa =
    1.0000   -0.8944    0.6954    0.9997   -0.8933    0.6949

Algorithm

By default, invfreqz uses an equation error method to identify the best model from the data. This finds b and a in

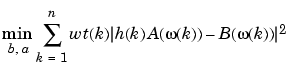
by creating a system of linear equations and solving them with the MATLAB \ operator. Here A((k)) and B((k)) are the Fourier transforms of the polynomials a and b, respectively, at the frequency (k), and n is the number of frequency points (the length of h and w). This algorithm is a based on Levi [1].

The superior ("output-error") algorithm uses the damped Gauss-Newton method for iterative search [2], with the output of the first algorithm as the initial estimate. This solves the direct problem of minimizing the weighted sum of the squared error between the actual and the desired frequency response points.

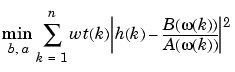
See Also

freqs, freqz, invfreqz, prony

References

[1] Levi, E.C., "Complex-Curve Fitting," IRE Trans. on Automatic Control, Vol. AC-4 (1959), pp. 37-44.

[2] Dennis, J.E., Jr., and R.B. Schnabel, Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Prentice-Hall, 1983.

invfreqs is2rc