residuez (Signal Processing Toolbox)

z-transform partial-fraction expansion

Syntax

[r,p,k] = residuez(b,a)
[b,a] = residuez(r,p,k)

Description

residuez converts a discrete time system, expressed as the ratio of two polynomials, to partial fraction expansion, or residue, form. It also converts the partial fraction expansion back to the original polynomial coefficients.

[r,p,k] = residuez(b,a) finds the residues, poles, and direct terms of a partial fraction expansion of the ratio of two polynomials, b(z) and a(z). Vectors b and a specify the coefficients of the polynomials of the discrete-time system b(z)/a(z) in descending powers of z.

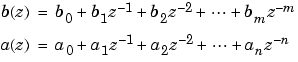
If there are no multiple roots and a > n-1,

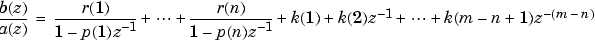
The returned column vector r contains the residues, column vector p contains the pole locations, and row vector k contains the direct terms. The number of poles is

n = length(a)-1 = length(r) = length(p)

The direct term coefficient vector k is empty if length(b) is less than length(a); otherwise:

length(k) = length(b) - length(a) + 1

If p(j) = ... = p(j+s-1) is a pole of multiplicity s, then the expansion includes terms of the form

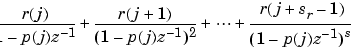
[b,a] = residuez(r,p,k) with three input arguments and two output arguments, converts the partial fraction expansion back to polynomials with coefficients in row vectors b and a.

The residue function in the standard MATLAB language is very similar to residuez. It computes the partial fraction expansion of continuous-time systems in the Laplace domain (see reference [1]), rather than discrete-time systems in the z-domain as does residuez.

Algorithm

residuez applies standard MATLAB functions and partial fraction techniques to find r, p, and k from b and a. It finds

The direct terms a using deconv (polynomial long division) when length(b) > length(a)-1.
The poles using p = roots(a).
Any repeated poles, reordering the poles according to their multiplicities.
The residue for each nonrepeating pole p_i by multiplying b(z)/a(z) by 1/(1 - p_iz^-1) and evaluating the resulting rational function at z = p_i.
The residues for the repeated poles by solving

```
S2*r2 = h - S1*r1
```

for r2 using \. h is the impulse response of the reduced b(z)/a(z), S1 is a matrix whose columns are impulse responses of the first-order systems made up of the nonrepeating roots, and r1 is a column containing the residues for the nonrepeating roots. Each column of matrix S2 is an impulse response. For each root p_j of multiplicity s_j, S2 contains s_j columns representing the impulse responses of each of the following systems.

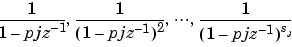
The vector h and matrices S1 and S2 have n + xtra rows, where n is the total number of roots and the internal parameter xtra, set to 1 by default, determines the degree of overdetermination of the system of equations.

See Also

convmtx, deconv, poly, prony, residue, roots, ss2tf, tf2ss, tf2zp, tf2zpk, zp2ss

References

[1] Oppenheim, A.V., and R.W. Schafer, Digital Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1975, pp. 166-170.

resample rlevinson