Vector Definition--Transition Scaling Values :: Demo: Vector Transition Processing Using Windows (Signal Processing Toolbox)

Signal Processing Toolbox

Vector Definition--Transition Scaling Values

These parameters define the normalization scaling to be applied to the basis functions to create a unit change in velocity and position. They depend directly on the other Vector Definition parameters:

K₀ -- scaling applied to zero-order basis function to produce the plotted vector transition.

K₁ -- scaling applied to first-order basis function to produce the plotted vector transition

Second Derivative Plot

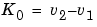
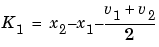
Select the plot to display on the Second Derivative axes:

Display Plots

Three plots are shown in the Vector Transition demo:

Vector Transition (Position) Plot

This plot is divided into three periods. The initial vector is on the left, the target vector is on the right, and the computed transition waveform is in between.

Modifying the window selection parameters creates a different transition.

Modifying the vector definition parameters changes the initial vector and/or the target vector. If either vector is modified, the transition waveform is rescaled to create a smoothed transition in position and velocity. A change to the vectors does not impact the transition basis function. It simply rescales the waveforms. Notice the changes in K1 and K0 when the vectors are modified.

First Derivative (Velocity) Plot

This plot is the first derivative of the vector transition waveform. In motion control applications, it corresponds to the velocity waveform. Generally the transition solution should produce a smooth transition between the initial and target velocities.

For this demo, the initial and target vectors are defined with constant velocities. Therefore, the period (t < 0)and target period (t > 1) will always be constant values equal to v1 and v2.

Second Derivative (Acceleration) Plot

Note Depending on the plot selected in Second Derivative Plot, you may see the Energy Spectra plot here.

This plot is the second derivative of the vector transition waveform. In motion control applications, it corresponds to the acceleration of the system.

The technique applied by this demo relies on two basis functions computed from windows, which are then applied as accelerations during the transition period. Thus, the acceleration during the transition is a linear combination of the basis functions. If the transition requires only a zero-order basis, the acceleration will be a scaled version of the selected window function. This occurs if the initial and target vectors have equal and opposite velocities (v1 + v2 = 0).

Selecting the sample vector Turn-Corner produces a scaled version of the selected window function. In a similar manner, you can view the first-order basis function by forcing initial and target velocities to be equal (v₁- v₂ = 0)).

Raster-X sample vector produces an acceleration plot using only the first-order basis function. Most other waveforms require a combination of zero-order and first-order terms.

Second Derivative (Energy Spectra) Plot

Note Depending on the plot selected in Second Derivative Plot, you may see the Acceleration plot here.

This plot is the spectrum of the acceleration. Often the goal of creating a smooth transition is to reduce the high-frequency content to avoid distortions when the waveform is passed through a band-limited or resonant system. Therefore, it is useful to examine the energy (single transition) or power content (repeated transitions) in a certain frequency band.

In many motion control applications, the acceleration is proportional to power, and correspondingly, the acceleration spectra is proportional to the energy spectra. The spectra plot is in dB and limited to frequencies less than 10/T where T is the transition period.

Vector Definition - Target Vector Definition Technical Conventions