besselh (MATLAB Functions)

Bessel function of the third kind (Hankel function)

Syntax

H = besselh(nu,K,Z)
H = besselh(nu,Z)
H = besselh(nu,K,Z,1)
[H,ierr] = besselh(...)

Definitions

The differential equation

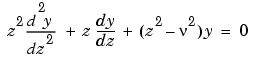
where 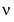is a nonnegative constant, is called Bessel's equation, and its solutions are known as Bessel functions. 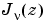and 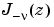form a fundamental set of solutions of Bessel's equation for noninteger 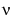. 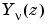is a second solution of Bessel's equation - linearly independent of 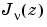- defined by

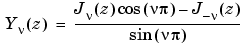
The relationship between the Hankel and Bessel functions is

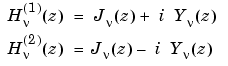
where 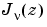is besselj, and 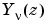is bessely.

Description

H = besselh(nu,K,Z) computes the Hankel function 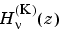, where K = 1 or 2, for each element of the complex array Z. If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, besselh expands it to the other input's size. If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

H = besselh(nu,Z) uses K = 1.

H = besselh(nu,K,Z,1) scales 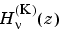by exp(-i*Z) if K = 1, and by exp(+i*Z) if K = 2.

[H,ierr] = besselh(...) also returns completion flags in an array the same size as H.

ierr
Description

0
besselh successfully computed the Hankel function for this element.

1
Illegal arguments.

2
Overflow. Returns Inf.

3
Some loss of accuracy in argument reduction.

4
Unacceptable loss of accuracy, Z or nu too large.

5
No convergence. Returns NaN.

ierr	Description
`0`	`besselh` successfully computed the Hankel function for this element.
`1`	Illegal arguments.
`2`	Overflow. Returns `Inf`.
`3`	Some loss of accuracy in argument reduction.
`4`	Unacceptable loss of accuracy, `Z` or `nu` too large.
`5`	No convergence. Returns `NaN`.

Examples

This example generates the contour plots of the modulus and phase of the Hankel function 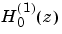shown on page 359 of [1] Abramowitz and Stegun, Handbook of Mathematical Functions.

It first generates the modulus contour plot

[X,Y] = meshgrid(-4:0.025:2,-1.5:0.025:1.5);
H = besselh(0,1,X+i*Y);
contour(X,Y,abs(H),0:0.2:3.2), hold on

then adds the contour plot of the phase of the same function.

contour(X,Y,(180/pi)*angle(H),-180:10:180); hold off

See Also

besselj, bessely, besseli, besselk

References

[1] Abramowitz, M. and I. A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965.

beep besseli