bessely (MATLAB Functions)

Bessel functions of the second kind

Syntax

Y = bessely(nu,Z)
Y = bessely(nu,Z,1)
[Y,ierr] = bessely(nu,Z)

Definition

The differential equation

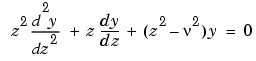
where 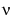is a real constant, is called Bessel's equation, and its solutions are known as Bessel functions.

A solution 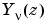of the second kind can be expressed as

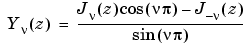
where 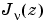and 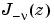form a fundamental set of solutions of Bessel's equation for noninteger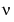

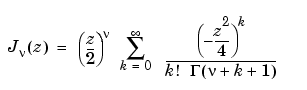
and 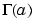is the gamma function. 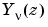is linearly independent of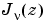

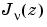can be computed using besselj.

Description

Y = bessely(nu,Z) computes Bessel functions of the second kind, 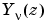, for each element of the array Z. The order nu need not be an integer, but must be real. The argument Z can be complex. The result is real where Z is positive.

If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, it is expanded to the other input's size. If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

Y = bessely(nu,Z,1) computes bessely(nu,Z).*exp(-abs(imag(Z))).

[Y,ierr] = bessely(nu,Z) also returns completion flags in an array the same size as Y.

ierr
Description

0
bessely successfully computed the Bessel function for this element.

1
Illegal arguments.

2
Overflow. Returns Inf.

3
Some loss of accuracy in argument reduction.

4
Unacceptable loss of accuracy, Z or nu too large.

5
No convergence. Returns NaN.

ierr	Description
`0`	`bessely` successfully computed the Bessel function for this element.
`1`	Illegal arguments.
`2`	Overflow. Returns `Inf`.
`3`	Some loss of accuracy in argument reduction.
`4`	Unacceptable loss of accuracy, `Z` or `nu` too large.
`5`	No convergence. Returns `NaN`.

Remarks

The Bessel functions are related to the Hankel functions, also called Bessel functions of the third kind,

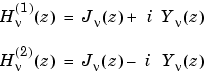
where 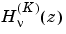is besselh, 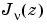is besselj, and 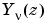is bessely. The Hankel functions also form a fundamental set of solutions to Bessel's equation (see besselh).

Examples

Example 1.

format long
z = (0:0.2:1)';

bessely(1,z)

ans =
               -Inf
  -3.32382498811185
  -1.78087204427005
  -1.26039134717739
  -0.97814417668336
  -0.78121282130029

Example 2. bessely(3:9,(0:.2:10)') generates the entire table on page 399 of [1] Abramowitz and Stegun, Handbook of Mathematical Functions.

Algorithm

The bessely function uses a Fortran MEX-file to call a library developed by D. E Amos [3] [4].

See Also

besselh, besseli, besselj, besselk

References

[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sections 9.1.1, 9.1.89 and 9.12, formulas 9.1.10 and 9.2.5.

[2] Carrier, Krook, and Pearson, Functions of a Complex Variable: Theory and Technique, Hod Books, 1983, section 5.5.

[3] Amos, D. E., "A Subroutine Package for Bessel Functions of a Complex Argument and Nonnegative Order," Sandia National Laboratory Report, SAND85-1018, May, 1985.

[4] Amos, D. E., "A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order," Trans. Math. Software, 1986.

besselk beta