besselk (MATLAB Functions)

Modified Bessel function of the second kind

Syntax

K = besselk(nu,Z)
K = besselk(nu,Z,1)
[K,ierr] = besselk(...)

Definitions

The differential equation

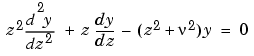
where 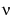is a real constant, is called the modified Bessel's equation, and its solutions are known as modified Bessel functions.

A solution 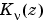of the second kind can be expressed as

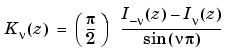
where 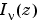and 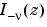form a fundamental set of solutions of the modified Bessel's equation for noninteger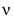

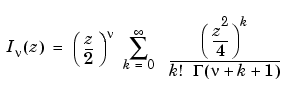
and 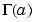is the gamma function. 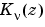is independent of .

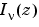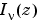can be computed using besseli.

Description

K = besselk(nu,Z) computes the modified Bessel function of the second kind, 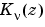, for each element of the array Z. The order nu need not be an integer, but must be real. The argument Z can be complex. The result is real where Z is positive.

If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, it is expanded to the other input's size. If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

K = besselk(nu,Z,1) computes besselk(nu,Z).*exp(Z).

[K,ierr] = besselk(...) also returns completion flags in an array the same size as K.

ierr
Description

0
besselk successfully computed the modified Bessel function for this element.

1
Illegal arguments.

2
Overflow. Returns Inf.

3
Some loss of accuracy in argument reduction.

4
Unacceptable loss of accuracy, Z or nu too large.

5
No convergence. Returns NaN.

ierr	Description
`0`	`besselk` successfully computed the modified Bessel function for this element.
`1`	Illegal arguments.
`2`	Overflow. Returns `Inf`.
`3`	Some loss of accuracy in argument reduction.
`4`	Unacceptable loss of accuracy, `Z` or `nu` too large.
`5`	No convergence. Returns `NaN`.

Examples

Example 1.

format long
z = (0:0.2:1)';

besselk(1,z)

ans =
                Inf
   4.77597254322047
   2.18435442473269
   1.30283493976350
   0.86178163447218
   0.60190723019723

Example 2. besselk(3:9,(0:.2:10)',1) generates part of the table on page 424 of [1] Abramowitz and Stegun, Handbook of Mathematical Functions.

Algorithm

The besselk function uses a Fortran MEX-file to call a library developed by D. E. Amos [3] [4].

See Also

airy, besselh, besseli, besselj, bessely

References

[1] Abramowitz, M. and I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, Applied Math. Series #55, Dover Publications, 1965, sections 9.1.1, 9.1.89 and 9.12, formulas 9.1.10 and 9.2.5.

[2] Carrier, Krook, and Pearson, Functions of a Complex Variable: Theory and Technique, Hod Books, 1983, section 5.5.

[3] Amos, D. E., "A Subroutine Package for Bessel Functions of a Complex Argument and Nonnegative Order," Sandia National Laboratory Report, SAND85-1018, May, 1985.

[4] Amos, D. E., "A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order," Trans. Math. Software, 1986.

besselj bessely