Windowing Method :: Filter Design and Implementation (Signal Processing Toolbox)

Signal Processing Toolbox

Windowing Method

Consider the ideal, or "brick wall," digital lowpass filter with a cutoff frequency of ₀ rad/s. This filter has magnitude 1 at all frequencies with magnitude less than ₀, and magnitude 0 at frequencies with magnitude between ₀ and 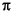. Its impulse response sequence h(n) is

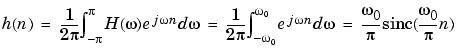
This filter is not implementable since its impulse response is infinite and noncausal. To create a finite-duration impulse response, truncate it by applying a window. By retaining the central section of impulse response in this truncation, you obtain a linear phase FIR filter. For example, a length 51 filter with a lowpass cutoff frequency ₀ of 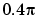rad/s is

```
b = 0.4*sinc(0.4*(-25:25));
```

The window applied here is a simple rectangular window. By Parseval's theorem, this is the length 51 filter that best approximates the ideal lowpass filter, in the integrated least squares sense. The following command displays the filter's frequency response in FVTool:

```
fvtool(b,1)
```

Note that the y-axis shown in the figure below is in Magnitude Squared. You can set this by right-clicking on the axis label and selecting Magnitude Squared from the menu.

Ringing and ripples occur in the response, especially near the band edge. This "Gibbs effect" does not vanish as the filter length increases, but a nonrectangular window reduces its magnitude. Multiplication by a window in the time domain causes a convolution or smoothing in the frequency domain. Apply a length 51 Hamming window to the filter and display the result using FVTool:

b = 0.4*sinc(0.4*(-25:25));
b = b.*hamming(51)';
fvtool(b,1)

Note that the y-axis shown in the figure below is in Magnitude Squared. You can set this by right-clicking on the axis label and selecting Magnitude Squared from the menu.

Using a Hamming window greatly reduces the ringing. This improvement is at the expense of transition width (the windowed version takes longer to ramp from passband to stopband) and optimality (the windowed version does not minimize the integrated squared error).

The functions fir1 and fir2 are based on this windowing process. Given a filter order and description of an ideal desired filter, these functions return a windowed inverse Fourier transform of that ideal filter. Both use a Hamming window by default, but they accept any window function. See the Windows for an overview of windows and their properties.

Standard Band FIR Filter Design: fir1

fir1 implements the classical method of windowed linear phase FIR digital filter design. It resembles the IIR filter design functions in that it is formulated to design filters in standard band configurations: lowpass, bandpass, highpass, and bandstop.

The statements

```
n = 50;
Wn = 0.4;
b = fir1(n,Wn);
```

create row vector b containing the coefficients of the order n Hamming-windowed filter. This is a lowpass, linear phase FIR filter with cutoff frequency Wn. Wn is a number between 0 and 1, where 1 corresponds to the Nyquist frequency, half the sampling frequency. (Unlike other methods, here Wn corresponds to the 6 dB point.) For a highpass filter, simply append the string 'high' to the function's parameter list. For a bandpass or bandstop filter, specify Wn as a two-element vector containing the passband edge frequencies; append the string 'stop' for the bandstop configuration.

b = fir1(n,Wn,window) uses the window specified in column vector window for the design. The vector window must be n+1 elements long. If you do not specify a window, fir1 applies a Hamming window.

Kaiser Window Order Estimation. The kaiserord function estimates the filter order, cutoff frequency, and Kaiser window beta parameter needed to meet a given set of specifications. Given a vector of frequency band edges and a corresponding vector of magnitudes, as well as maximum allowable ripple, kaiserord returns appropriate input parameters for the fir1 function.

Multiband FIR Filter Design: fir2

The fir2 function also designs windowed FIR filters, but with an arbitrarily shaped piecewise linear frequency response. This is in contrast to fir1, which only designs filters in standard lowpass, highpass, bandpass, and bandstop configurations.

The commands

n = 50;
f = [0 .4 .5 1];
m = [1  1  0 0];
b = fir2(n,f,m);

return row vector b containing the n+1 coefficients of the order n FIR filter whose frequency-magnitude characteristics match those given by vectors f and m. f is a vector of frequency points ranging from 0 to 1, where 1 represents the Nyquist frequency. m is a vector containing the desired magnitude response at the points specified in f. (The IIR counterpart of this function is yulewalk, which also designs filters based on arbitrary piecewise linear magnitude responses. See IIR Filter Design for details.)

Linear Phase Filters Multiband FIR Filter Design with Transition Bands