fir2 (Signal Processing Toolbox)

Ffrequency sampling-based finite impulse response filter design

Syntax

b = fir2(n,f,m)
b = fir2(n,f,m,window)
b = fir2(n,f,m,npt)
b = fir2(n,f,m,npt,window)
b = fir2(n,f,m,npt,lap)
b = fir2(n,f,m,npt,lap,window)

Description

fir2 designs frequency sampling-based digital FIR filters with arbitrarily shaped frequency response.

Note Use fir1 for windows-based standard lowpass, bandpass, highpass, and bandstop configurations.

b = fir2(n,f,m) returns row vector b containing the n+1 coefficients of an order n FIR filter. The frequency-magnitude characteristics of this filter match those given by vectors f and m:

f is a vector of frequency points in the range from 0 to 1, where 1 corresponds to the Nyquist frequency. The first point of f must be 0 and the last point 1. The frequency points must be in increasing order.
m is a vector containing the desired magnitude response at the points specified in f.
f and m must be the same length.
Duplicate frequency points are allowed, corresponding to steps in the frequency response.

Use plot(f,m) to view the filter shape.

The output filter coefficients, b, are ordered in descending powers of z.

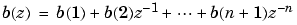
fir2 always uses an even filter order for configurations with a passband at the Nyquist frequency. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, fir2 increments it by 1.

b = fir2(n,f,m,window) uses the window specified in the column vector window. The vector window must be n+1 elements long. If no window is specified, fir2 uses a Hamming window (see hamming) of length n+1.

b = fir2(n,f,m,npt) or

b = fir2(n,f,m,npt,window) specifies the number of points, npt, for the grid onto which fir2 interpolates the frequency response, without or with a window specification.

b = fir2(n,f,m,npt,lap) and

b = fir2(n,f,m,npt,lap,window) specify the size of the region, lap, that fir2 inserts around duplicate frequency points, with or without a window specification.

See the "Algorithm" section for more on npt and lap.

Examples

Design a 30th-order lowpass filter and overplot the desired frequency response with the actual frequency response:

f = [0 0.6 0.6 1]; m = [1 1 0 0];
b = fir2(30,f,m);
[h,w] = freqz(b,1,128);
plot(f,m,w/pi,abs(h))
legend('Ideal','fir2 Designed')
title('Comparison of Frequency Response Magnitudes')

The resulting plot has the ideal response equal to one from 0 to 0.6. At 0.6, the response drops instantaneously to 0. The response designed using fir2 equals one from 0 to 0.5 and then decreases to zero, which it reaches at approximately 0.7.

Algorithm

The desired frequency response is interpolated onto a dense, evenly spaced grid of length npt. npt is 512 by default. If two successive values of f are the same, a region of lap points is set up around this frequency to provide a smooth but steep transition in the requested frequency response. By default, lap is 25. The filter coefficients are obtained by applying an inverse fast Fourier transform to the grid and multiplying by a window; by default, this is a Hamming window.

See Also

butter, cheby1, cheby2, ellip, fir1, maxflat, firpm, yulewalk

References

Mitra, S.K., Digital Signal Processing A Computer Based Approach, First Edition, McGraw-Hill, New York, 1998, pp. 462-468.

Jackson, L.B., Digital Filters and Signal Processing, Third Edition, Kluwer Academic Publishers, Boston, 1996, pp. 301-307.

fir1 fircls