rooteig (Signal Processing Toolbox)

Frequency and power content using eigenvector method

Syntax

[w,pow] = rooteig(x,p)
[f,pow] = rooteig(...,fs)
[w,pow] = rooteig(...,'corr')

Description

[w,pow] = rooteig(x,p) estimates the frequency content in the time samples of a signal x, and returns w, a vector of frequencies in rad/sample, and the corresponding signal power in the vector pow in units of power, such as volts^2. The input signal x is specified either as:

A row or column vector representing one observation of the signal
A rectangular array for which each row of x represents a separate observation of the signal (for example, each row is one output of an array of sensors, as in array processing), such that x'*x is an estimate of the correlation matrix

Note You can use the output of corrmtx to generate such an array x.

You can specify the second input argument p as either:

A scalar integer. In this case, the signal subspace dimension is p.
A two-element vector. In this case, p(2), the second element of p, represents a threshold that is multiplied by 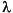_min, the smallest estimated eigenvalue of the signal's correlation matrix. Eigenvalues below the threshold 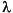_min*p(2) are assigned to the noise subspace. In this case, p(1) specifies the maximum dimension of the signal subspace.

The extra threshold parameter in the second entry in p provides you more flexibility and control in assigning the noise and signal subspaces.

The length of the vector w is the computed dimension of the signal subspace. For real-valued input data x, the length of the corresponding power vector pow is given by

```
length(pow) = 0.5*length(w)
```

For complex-valued input data x, pow and w have the same length.

[f,pow] = rooteig(...,fs) returns the vector of frequencies f calculated in Hz. You supply the sampling frequency fs in Hz. If you specify fs with the empty vector [], the sampling frequency defaults to 1 Hz.

[w,pow] = rooteig(...,'corr') forces the input argument x to be interpreted as a correlation matrix rather than a matrix of signal data. For this syntax, you must supply a square matrix for x, and all of its eigenvalues must be nonnegative.

Note You can place the string 'corr' anywhere after p.

Examples

Find the frequency content in a signal composed of three complex exponentials in noise. Use the modified covariance method to estimate the correlation matrix used by the eigenvector method:

randn('state',1); n=0:99;   
s = exp(i*pi/2*n)+2*exp(i*pi/4*n)+exp(i*pi/3*n)+randn(1,100); 
% Estimate correlation matrix using modified covariance method.
X=corrmtx(s,12,'mod'); 
[W,P] = rooteig(X,3)
W =
    0.7811
    1.5767
    1.0554
P =
    3.9971
    1.1362
    1.4102

Algorithm

The eigenvector method used by rooteig is the same as that used by peig. The algorithm performs eigenspace analysis of the signal's correlation matrix in order to estimate the signal's frequency content.

The difference between peig and rooteig is:

peig returns the pseudospectrum at all frequency samples.
rooteig returns the estimated discrete frequency spectrum, along with the corresponding signal power estimates.

rooteig is most useful for frequency estimation of signals made up of a sum of sinusoids embedded in additive white Gaussian noise.

See Also

corrmtx, peig, pmusic, powerest method of spectrum, rootmusic, spectrum.eigenvector

rlevinson rootmusic