peig (Signal Processing Toolbox)

Pseudospectrum using eigenvector method

Syntax

[S,w] = peig(x,p)
[S,w] = peig(...,nfft)
[S,f] = peig(x,p,nfft,fs)
[S,f] = peig(...,'corr')
[S,f] = peig(x,p,nfft,fs,nwin,noverlap)
[...] = peig(...,'range')
[...,v,e] = peig(...)
peig(...)

Description

[S,w] = peig(x,p) implements the eigenvector spectral estimation method and returns S, the pseudospectrum estimate of the input signal x, and w, a vector of normalized frequencies (in rad/sample) at which the pseudospectrum is evaluated. The pseudospectrum is calculated using estimates of the eigenvectors of a correlation matrix associated with the input data x, where x is specified as either:

A row or column vector representing one observation of the signal
A rectangular array for which each row of x represents a separate observation of the signal (for example, each row is one output of an array of sensors, as in array processing), such that x'*x is an estimate of the correlation matrix

Note You can use the output of corrmtx to generate such an array x.

You can specify the second input argument p as either:

A scalar integer. In this case, the signal subspace dimension is p.
A two-element vector. In this case, p(2), the second element of p, represents a threshold that is multiplied by 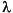_min, the smallest estimated eigenvalue of the signal's correlation matrix. Eigenvalues below the threshold 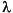_min*p(2) are assigned to the noise subspace. In this case, p(1) specifies the maximum dimension of the signal subspace.

The extra threshold parameter in the second entry in p provides you more flexibility and control in assigning the noise and signal subspaces.

S and w have the same length. In general, the length of the FFT and the values of the input x determine the length of the computed S and the range of the corresponding normalized frequencies. The following table indicates the length of S (and w) and the range of the corresponding normalized frequencies for this syntax.

S Characteristics for an FFT Length of 256 (Default)
Real/Complex Input Data
Length of S and w
Range of the Corresponding Normalized Frequencies

Real-valued
129
[0, ]

Complex-valued
256
[0, 2)

**S Characteristics for an FFT Length of 256 (Default)**
Real/Complex Input Data	Length of S and w	Range of the Corresponding Normalized Frequencies
Real-valued	129	[0, ]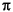
Complex-valued	256	[0, 2)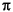

[S,w] = peig(...,nfft) specifies the length of the FFT used to estimate the pseudospectrum with the integer nfft. The default value for nfft (entered as an empty vector []) is 256.

The following table indicates the length of S and w, and the frequency range for w for this syntax.

S and Frequency Vector Characteristics
Real/Complex Input Data
nfft Even/Odd
Length of S and w
Range of w

Real-valued
Even
(nfft/2 + 1)
[0, ]

Real-valued
Odd
(nfft + 1)/2
[0, )

Complex-valued
Even or odd
nfft
[0, 2)

**S and Frequency Vector Characteristics**
Real/Complex Input Data	nfft Even/Odd	Length of S and w	Range of w
Real-valued	Even	`(nfft/2 + 1)`	[0, ]
Real-valued	Odd	`(nfft + 1)/2`	[0, )
Complex-valued	Even or odd	`nfft`	[0, 2)

[S,f] = peig(x,p,nfft,fs)) returns the pseudospectrum in the vector S evaluated at the corresponding vector of frequencies f (in Hz). You supply the sampling frequency fs in Hz. If you specify fs with the empty vector [], the sampling frequency defaults to 1 Hz.

The frequency range for f depends on nfft, fs, and the values of the input x. The length of S (and f) is the same as in the Table , S and Frequency Vector Characteristics above. The following table indicates the frequency range for f for this syntax.

S and Frequency Vector Characteristics with fs Specified
Real/Complex Input Data
nfft Even/Odd
Range of f

Real-valued
Even
[0,fs/2]

Real-valued
Odd
[0,fs/2)

Complex-valued
Even or odd
[0,fs)

**S and Frequency Vector Characteristics with fs Specified**
Real/Complex Input Data	nfft Even/Odd	Range of f
Real-valued	Even	`[0,fs/2]`
Real-valued	Odd	`[0,fs/2)`
Complex-valued	Even or odd	`[0,fs)`

[S,f] = peig(...,'corr') forces the input argument x to be interpreted as a correlation matrix rather than matrix of signal data. For this syntax x must be a square matrix, and all of its eigenvalues must be nonnegative.

[S,f] = peig(x,p,nfft,fs,nwin,noverlap) allows you to specify nwin, a scalar integer indicating a rectangular window length, or a real-valued vector specifying window coefficients. Use the scalar integer noverlap in conjunction with nwin to specify the number of input sample points by which successive windows overlap. noverlap is not used if x is a matrix. The default value for nwin is 2*p(1) and noverlap is nwin-1.

With this syntax, the input data x is segmented and windowed before the matrix used to estimate the correlation matrix eigenvalues is formulated. The segmentation of the data depends on nwin, noverlap, and the form of x. Comments on the resulting windowed segments are described in the following table.

Windowed Data Depending on x and nwin
Input data x
Form of nwin
Windowed Data

Data vector
Scalar
Length is nwin

Data vector
Vector of coefficients
Length is length(nwin)

Data matrix
Scalar
Data is not windowed.

Data matrix
Vector of coefficients
length(nwin) must be the same as the column length of x, and noverlap is not used.

**Windowed Data Depending on x and nwin**
Input data x	Form of nwin	Windowed Data
Data vector	Scalar	Length is `nwin`
Data vector	Vector of coefficients	`Length is length(nwin)`
Data matrix	Scalar	Data is not windowed.
Data matrix	Vector of coefficients	length(nwin) must be the same as the column length of `x`, and `noverlap` is not used.

See the Table , Eigenvector Length Depending on Input Data and Syntax below for related information on this syntax.

Note The arguments nwin and noverlap are ignored when you include the string 'corr' in the syntax.

[...] = peig(...,'range') specifies the range of frequency values to include in f or w. This syntax is useful when x is real. 'range' can be either:

'whole': Compute the pseudospectrum over the frequency range [0,fs). This is the default for determining the frequency range for complex-valued x.

If you specify fs as the empty vector, [], the frequency range is [0,1).
If you don't specify fs, the frequency range is [0, 2).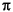

'half': Compute the pseudospectrum over the frequency ranges specified for real x. This is the default for determining the frequency range for real-valued x.

Note You can put the string arguments 'range' or 'corr' anywhere in the input argument list after p.

[...,v,e] = peig(...) returns the matrix v of noise eigenvectors, along with the associated eigenvalues in the vector e. The columns of v span the noise subspace of dimension size(v,2). The dimension of the signal subspace is size(v,1)-size(v,2). For this syntax, e is a vector of estimated eigenvalues of the correlation matrix.

peig(...) with no output arguments plots the pseudospectrum in the current figure window.

Remarks

In the process of estimating the pseudospectrum, peig computes the noise and signal subspaces from the estimated eigenvectors v_jand eigenvalues 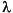lambda _j of the signal's correlation matrix. The smallest of these eigenvalues is used in conjunction with the threshold parameter p(2) to affect the dimension of the noise subspace in some cases.

The length n of the eigenvectors computed by peig is the sum of the dimensions of the signal and noise subspaces. This eigenvector length depends on your input (signal data or correlation matrix) and the syntax you use.

The following table summarizes the dependency of the eigenvector length on the input argument.

Eigenvector Length Depending on Input Data and Syntax
Form of Input Data x
Comments on the Syntax
Length n of Eigenvectors

Row or column vector
nwin is specified as a scalar integer.
nwin

Row or column vector
nwin is specified as a vector.
length(nwin)

Row or column vector
nwin is not specified.
2*p(1)

l-by-m matrix
If nwin is specified as a scalar, it is not used. If nwin is specified as a vector, length(nwin) must equal m.
m

m-by-m nonnegative definite matrix
The string 'corr' is specified and nwin is not used.
m

**Eigenvector Length Depending on Input Data and Syntax**
Form of Input Data x	Comments on the Syntax	Length n of Eigenvectors
Row or column vector	`nwin` is specified as a scalar integer.	`nwin`
Row or column vector	`nwin` is specified as a vector.	`length(nwin)`
Row or column vector	`nwin` is not specified.	`2*p(1)`
l-by-m matrix	If `nwin` is specified as a scalar, it is not used. If `nwin` is specified as a vector, `length(nwin)` must equal m.	m
m-by-m nonnegative definite matrix	The string `'corr'` is specified and `nwin` is not used.	m

You should specify nwin > p(1) or length(nwin) > p(1) if you want p(2) > 1 to have any effect.

Examples

Implement the eigenvector method to find the pseudospectrum of the sum of three sinusoids in noise, using the default FFT length of 256. Use the modified covariance method for the correlation matrix estimate:

randn('state',1); n=0:99;   
s=exp(i*pi/2*n)+2*exp(i*pi/4*n)+exp(i*pi/3*n)+randn(1,100);  
X=corrmtx(s,12,'mod'); 
peig(X,3,'whole')        % Uses the default NFFT of 256.

Algorithm

The eigenvector method estimates the pseudospectrum from a signal or a correlation matrix using a weighted version of the MUSIC algorithm derived from Schmidt's eigenspace analysis method [1][2]. The algorithm performs eigenspace analysis of the signal's correlation matrix in order to estimate the signal's frequency content. The eigenvalues and eigenvectors of the signal's correlation matrix are estimated using svd if you don't supply the correlation matrix. This algorithm is particularly suitable for signals that are the sum of sinusoids with additive white Gaussian noise.

The eigenvector method produces a pseudospectrum estimate given by

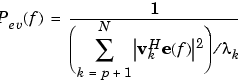
where N is the dimension of the eigenvectors and v_kis the kth eigenvector of the correlation matrix of the input signal. The integer p is the dimension of the signal subspace, so the eigenvectors v_k used in the sum correspond to the smallest eigenvalues 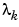of the correlation matrix. The eigenvectors used in the PSD estimate span the noise subspace. The vector e(f) consists of complex exponentials, so the inner product

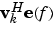
amounts to a Fourier transform. This is used for computation of the PSD estimate. The FFT is computed for each v_k and then the squared magnitudes are summed and scaled.

See Also

corrmtx, pburg, periodogram, pmtm, pmusic, prony, pwelch, rooteig, rootmusic

References

[1] Marple, S.L. Digital Spectral Analysis, Englewood Cliffs, NJ, Prentice-Hall, 1987, pp. 373-378.

[2] Schmidt, R.O, "Multiple Emitter Location and Signal Parameter Estimation," IEEE Trans. Antennas Propagation, Vol. AP-34 (March 1986), pp. 276-280.

[3] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, 1997.

pcov periodogram