Signal Processing Toolbox

Vector Transition Demo

In any system where you need to connect two vectors (any straight lines) with a smooth path, the optimal choice for vector transition is one with characteristics matched to the system. Spectral windows are one technique for creating transition solutions to match bandlimited or resonant systems. By using a spectral window, we can compute a solution for any vector transition. The window-based approach demonstrated below requires two waveforms:

• Awaveform of any spectral window available in MATLAB
• A waveform derived from that spectral window

With this method, you can create a solution that minimizes discontinuities, particularly for smooth windows such as the hann, nuttallwin, and blackman. In systems with limited bandwidth and resonance frequencies, applying these smoothed transitions can reduce the settling time. You can see the reduction in high-frequency content in the windowed solution versus the direct path by selecting Energy Spectra in Second Derivative Plot. The direct solution creates impulses in acceleration, which means lots of high-frequency content.

For background information, see Vector Transition Demo--Background Information and for a specific example to try, see Example--Airplane Takeoff.

Window Selection

This area defines the window function to be used to create a smoothed vector transition path. Window selection parameters are:

• Pull-down menu
• Parameter
• First-Order Method
• Window Scaling Values

From the selected window, two orthogonal, reference waveforms (basis functions) are generated. These are used to shape a smooth, continuous vector transition with no discontinuities in position or velocity. The generated waveforms are defined in acceleration space (second-derivative of the position). Most window functions produce interesting and potentially useful results. Some windows, such as Chebyshev, are not well suited to the task.

Window Selection--Pull-Down Menu

Select a window function to create a smoothed vector transition path. All window functions provided by the Signal Processing Toolbox are included. The choice of window affects the path defined in the Vector Transition (Position) plot from 0 < t < 1.

The window selected in this menu is scaled to become the zero-order function, which is one of the basis functions required to create a smooth transition. Most windows in the Signal Processing Toolbox satisfy the boundary conditions required to produce a smooth vector transition. Refer to Vector Transition Demo--Background Information for information on windows that do not produce smooth transitions.

Window Selection--Parameter

This is enabled if the selected window function requires an additional numeric parameter. Refer to the documentation for each window for details on the effects of this parameter.

Window Selection--First-Order Method

The function to be derived from the selected window function. Select the technique to generate the first-order window.

Sine	Wf0 = W(N)*sin(linspace(0,2*pi,N))
Derivative	Wf0 = [0; diff(W(N-1)); 0]
Mirror	Wf0 = [W(N/2); -1*W(N/2)]

The method shown here is used with the selected window to compute the first-order waveform. This waveform is one of the basis functions required to create a smooth transition.

Window Selection--Window Scaling Values

Scaling is used to create a seamless transition between vector positions and velocities. These two scaling terms apply to the window:

• W₀ -- scaling term applied to the selected window (applied to an acceleration term) to produce a unit change in velocity.

• W₁ -- scaling term applied to the first-order acceleration function to produce a unit change in position.

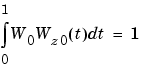
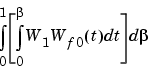
Vector Definition

The path made by the windowing function must be scaled to fit the initial and target vectors. Vector definition parameters are:

• Sample Vectors
• Initial Vector Definition
• Target Vector Definition
• Transition Scaling Values

Example--Airplane Takeoff

Vector Definition--Sample Vectors

© 1994-2005 The MathWorks, Inc.