

| Signal Processing Toolbox |   |
Power spectral density using Burg method
Syntax
Pxx = pburg(x,p) [Pxx,w] = pburg(x,p) [Pxx,w]=pburg(x,p,nfft) [Pxx,f]=pburg(x,p,nfft,fs) [Pxx,f]=pburg(x,p,nfft,fs,'range') [Pxx,w]=pburg(x,p,nfft,'range') pburg(...)
Description
Pxx implements the Burg algorithm, a parametric spectral estimation method, and returns = pburg(x,p)
Pxx, an estimate of the power spectral density (PSD) of the vector x. The entries of x represent samples of a discrete-time signal, and p is the integer specifying the order of an autoregressive (AR) prediction model for the signal, used in estimating the PSD.
The power spectral density is calculated in units of power per radians per sample. Real-valued inputs produce full power one-sided (in frequency) PSDs (by default), while complex-valued inputs produce two-sided PSDs.
In general, the length of the FFT and the values of the input x determine the length of Pxx and the range of the corresponding normalized frequencies. For this syntax, the (default) FFT length is 256. The following table indicates the length of Pxx and the range of the corresponding normalized frequencies for this syntax.
| Real/Complex Input Data |
Length of Pxx |
Range of the Corresponding Normalized Frequencies |
| Real-valued |
129 |
[0, 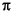 ] ] |
| Complex-valued |
256 |
[0, 2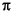 ) ) |
[Pxx,w] also returns = pburg(x,p)
w, a vector of frequencies at which the PSD is estimated. Pxx and w have the same length. The units for frequency are rad/sample.
[Pxx,w] uses the Burg method to estimate the PSD while specifying the length of the FFT with the integer = pburg(x,p,nfft)
nfft. If you specify nfft as the empty vector [], it takes the default value of 256.
The length of Pxx and the frequency range for w depend on nfft and the values of the input x. The following table indicates the length of Pxx and the frequency range for w in this syntax.
[Pxx,f] uses the sampling frequency = pburg(x,p,nfft,fs)
fs specified as an integer in hertz (Hz) to compute the PSD vector (Pxx) and the corresponding vector of frequencies (f). In this case, the units for the frequency vector are in Hz. The spectral density produced is calculated in units of power per Hz. If you specify fs as the empty vector [], the sampling frequency defaults to 1 Hz.
The frequency range for f depends on nfft, fs, and the values of the input x. The length of Pxx is the same as in the table above. The following table indicates the frequency range for f for this syntax.
| Real/Complex Input Data |
nfft Even/Odd |
Range of f |
| Real-valued |
Even |
[0,fs/2] |
| Real-valued |
Odd |
[0,fs/2) |
| Complex-valued |
Even or odd |
[0,fs) |
[Pxx,f] or = pburg(x,p,nfft,fs,'range')
[Pxx,w] specifies the range of frequency values to include in = pburg(x,p,nfft,'range')
f or w. This syntax is useful when x is real. 'range' can be either:
'twosided': Compute the two-sided PSD over the frequency range [0,fs). This is the default for determining the frequency range for complex-valued x.
fs as the empty vector, [], the frequency range is [0,1).
fs, the frequency range is [0, 2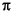 ).
).
'onesided': Compute the one-sided PSD over the frequency ranges specified for real x. This is the default for determining the frequency range for real-valued x.
pburg(...)
with no outputs plots the power spectral density in the current figure window. The frequency range on the plot is the same as the range of output w (or f) for a given set of parameters.
Remarks
The power spectral density is computed as the distribution of power per unit frequency.
This algorithm depends on your selecting an appropriate model order for your signal.
Examples
Because the Burg method estimates the spectral density by fitting an AR prediction model of a given order to the signal, first generate a signal from an AR (all-pole) model of a given order. You can use freqz to check the magnitude of the frequency response of your AR filter. This will give you an idea of what to expect when you estimate the PSD using pburg:
a = [1 -2.2137 2.9403 -2.1697 0.9606]; % AR filter coefficients
freqz(1,a) % AR filter frequency response
title('AR System Frequency Response')
Now generate the input signal x by filtering white noise through the AR filter. Estimate the PSD of x based on a fourth-order AR prediction model since in this case we know that the original AR system model a has order 4:
randn('state',1);
x = filter(1,a,randn(256,1)); % AR system output
pburg(x,4) % Fourth-order estimate
Algorithm
Linear prediction filters can be used to model the second-order statistical characteristics of a signal. The prediction filter output can be used to model the signal when the input is white noise.
The Burg method fits an AR linear prediction filter model of the specified order to the input signal by minimizing (using least squares) the arithmetic mean of the forward and backward prediction errors. The spectral density is then computed from the frequency response of the prediction filter. The AR filter parameters are constrained to satisfy the Levinson-Durbin recursion.
See Also
arburg, lpc, pcov, peig, periodogram, pmcov, pmtm, pmusic, pwelch, pyulear
References
[1] Marple, S.L. Digital Spectral Analysis, Englewood Cliffs, NJ, Prentice-Hall, 1987, Chapter 7.
[2] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, 1997.
 | parzenwin | pcov |  |
© 1994-2005 The MathWorks, Inc.