Signal Processing Toolbox

pmcov

Power spectral density using modified covariance method

Syntax

• Pxx = pmcov(x,p)
  [Pxx,w] = pmcov(x,p)
  [Pxx,w] = pmcov(x,p,nfft)
  [Pxx,f] = pmcov(x,p,nfft,fs)
  [Pxx,f] = pmcov(x,p,nfft,fs,'range')
  [Pxx,w] = pmcov(x,p,nfft,'range')
  pmcov(...)
  

Description

Pxx = pmcov(x,p) implements the modified covariance algorithm, a parametric spectral estimation method, and returns Pxx, an estimate of the power spectral density (PSD) of the vector x. The entries of x represent samples of a discrete-time signal, and p is the integer specifying the order of an autoregressive (AR) prediction model for the signal, used in estimating the PSD.

The power spectral density is calculated in units of power per radians per sample. Real-valued inputs produce full power one-sided (in frequency) PSDs (by default), while complex-valued inputs produce two-sided PSDs.

In general, the length of the FFT and the values of the input x determine the length of Pxx and the range of the corresponding normalized frequencies. For this syntax, the (default) FFT length is 256. The following table indicates the length of Pxx and the range of the corresponding normalized frequencies for this syntax.

PSD Vector Characteristics for an FFT Length of 256 (Default)

Real/Complex Input Data	Length of Pxx	Range of the Corresponding Normalized Frequencies
Real-valued	129	[0, ]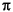
Complex-valued	256	[0, 2)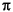

[Pxx,w] = pmcov(x,p) also returns w, a vector of frequencies at which the PSD is estimated. Pxx and w have the same length. The units for frequency are rad/sample.

[Pxx,w] = pmcov(x,p,nfft) uses the covariance method to estimate the PSD while specifying the length of the FFT with the integer nfft. If you specify nfft as the empty vector [], it takes the default value of 256.

The length of Pxx and the frequency range for w depend on nfft and the values of the input x. The following table indicates the length of Pxx and the frequency range for w for this syntax.

PSD and Frequency Vector Characteristics

Real/Complex Input Data	nfft Even/Odd	Length of Pxx	Range of w
Real-valued	Even	(nfft/2 + 1)	[0, ]
Real-valued	Odd	(nfft + 1)/2	[0, )
Complex-valued	Even or odd	nfft	[0, 2)

[Pxx,f] = pmcov(x,p,nfft,fs) uses the sampling frequency fs specified as an integer in hertz (Hz) to compute the PSD vector (Pxx) and the corresponding vector of frequencies (f). In this case, the units for the frequency vector are in Hz. The spectral density produced is calculated in units of power per Hz. If you specify fs as the empty vector [], the sampling frequency defaults to 1 Hz.

The frequency range for f depends on nfft, fs, and the values of the input x. The length of Pxx is the same as in the Table , PSD and Frequency Vector Characteristics above. The following table indicates the frequency range for f in this syntax.

PSD and Frequency Vector Characteristics with fs Specified

Real/Complex Input Data	nfft Even/Odd	Range of f
Real-valued	Even	[0,fs/2]
Real-valued	Odd	[0,fs/2)
Complex-valued	Even or odd	[0,fs)

[Pxx,f] = pmcov(x,p,nfft,fs,'range') or

[Pxx,w] = pmcov(x,p,nfft,'range') specifies the range of frequency values to include in f or w. This syntax is useful when x is real. 'range' can be either:

• 'twosided': Compute the two-sided PSD over the frequency range [0,fs). This is the default for determining the frequency range for complex-valued x.
• If you specify fs as the empty vector, [], the frequency range is [0,1).
• If you don't specify fs, the frequency range is [0, 2).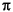
• 'onesided': Compute the one-sided PSD over the frequency ranges specified for real x. This is the default for determining the frequency range for real-valued x.

Note    You can put the string argument 'range' anywhere in the input argument list after p.

pmcov(...) with no outputs plots the power spectral density in the current figure window. The frequency range on the plot is the same as the range of output w (or f) for a given set of parameters.

Remarks

The power spectral density is computed as the distribution of power per unit frequency.

This algorithm depends on your selecting an appropriate model order for your signal.

Examples

Because the modified covariance method estimates the spectral density by fitting an AR prediction model of a given order to the signal, first generate a signal from an AR (all-pole) model of a given order. You can use freqz to check the magnitude of the frequency response of your AR filter. This will give you an idea of what to expect when you estimate the PSD using pmcov:

• a = [1 -2.2137 2.9403 -2.1697 0.9606];  % AR filter coefficients
  freqz(1,a)  % AR filter frequency response
  title('AR System Frequency Response')
  
  
  

Now generate the input signal x by filtering white noise through the AR filter. Estimate the PSD of x based on a fourth-order AR prediction model since in this case we know that the original AR system model a has order 4:

• randn('state',1);
  x = filter(1,a,randn(256,1));    % AR filter output
  pmcov(x,4)                       % Fourth-order estimate
  
  
  

Algorithm

Linear prediction filters can be used to model the second-order statistical characteristics of a signal. The prediction filter output can be used to model the signal when the input is white noise.

pmcov estimates the PSD of the signal vector using the modified covariance method. This method fits an autoregressive (AR) linear prediction filter model to the signal by simultaneously minimizing the forward and backward prediction errors (based on causal observations of your input signal) in the least squares sense. The spectral estimate returned by pmcov is the magnitude squared frequency response of this AR model.

See Also

armcov, lpc, pburg, pcov, peig, periodogram, pmtm, pmusic, pwelch, prony, pyulear

References

[1] Marple, S.L. Digital Spectral Analysis, Englewood Cliffs, NJ, Prentice-Hall, 1987, Chapter 7.

[2] Stoica, P., and R.L. Moses, Introduction to Spectral Analysis, Prentice-Hall, 1997.

phasez

pmtm

© 1994-2005 The MathWorks, Inc.