yulewalk (Signal Processing Toolbox)

Signal Processing Toolbox

yulewalk

Recursive digital filter design

Syntax

```
[b,a] = yulewalk(n,f,m)
```

Description

yulewalk designs recursive IIR digital filters using a least-squares fit to a specified frequency response.

[b,a] = yulewalk(n,f,m) returns row vectors b and a containing the n+1 coefficients of the order n IIR filter whose frequency-magnitude characteristics approximately match those given in vectors f and m:

f is a vector of frequency points, specified in the range between 0 and 1, where 1 corresponds to half the sample frequency (the Nyquist frequency). The first point of f must be 0 and the last point 1, with all intermediate points in increasing order. Duplicate frequency points are allowed, corresponding to steps in the frequency response.
m is a vector containing the desired magnitude response at the points specified in f.
f and m must be the same length.
plot(f,m) displays the filter shape.

The output filter coefficients are ordered in descending powers of z.

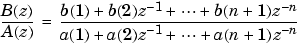
When specifying the frequency response, avoid excessively sharp transitions from passband to stopband. You may need to experiment with the slope of the transition region to get the best filter design.

Examples

Design an 8th-order lowpass filter and overplot the desired frequency response with the actual frequency response:

f = [0 0.6 0.6 1];
m = [1 1 0 0];

[b,a] = yulewalk(8,f,m);
[h,w] = freqz(b,a,128);
plot(f,m,w/pi,abs(h),'--')
legend('Ideal','yulewalk Designed')
title('Comparison of Frequency Response Magnitudes')

Algorithm

yulewalk performs a least-squares fit in the time domain. It computes the denominator coefficients using modified Yule-Walker equations, with correlation coefficients computed by inverse Fourier transformation of the specified frequency response. To compute the numerator, yulewalk takes the following steps:

Computes a numerator polynomial corresponding to an additive decomposition of the power frequency response.
Evaluates the complete frequency response corresponding to the numerator and denominator polynomials.
Uses a spectral factorization technique to obtain the impulse response of the filter.
Obtains the numerator polynomial by a least-squares fit to this impulse response.

See Also

butter, cheby1, cheby2, ellip, fir2, firls, maxflat, firpm

References

[1] Friedlander, B., and B. Porat, "The Modified Yule-Walker Method of ARMA Spectral Estimation," IEEE Transactions on Aerospace Electronic Systems, AES-20, No. 2 (March 1984), pp. 158-173.

xcov zerophase