

| Wavelet Toolbox |   |
Functions -- Categorical List
Graphical User Interface Tools
|
Wavelet graphical user interface tools |
General Wavelet Functions
|
Biorthogonal wavelet filter set |
|
Wavelet center frequency |
|
Dyadic downsampling |
|
Dyadic upsampling |
|
Integrate wavelet function psi (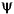 ) ) |
|
Orthogonal wavelet filter set |
|
Quadrature mirror filter |
|
Scale to frequency |
|
Wavelet and scaling functions |
|
Wavelet and scaling functions 2-D |
|
Wavelet manager |
|
Wavelet filters |
|
Maximum wavelet decomposition level |
Wavelet Families
|
Biorthogonal spline wavelet filters |
|
Complex Gaussian wavelet |
|
Complex Morlet wavelet |
|
Coiflet wavelet filter |
|
Daubechies wavelet filter computation |
|
Daubechies wavelet filter |
|
Complex frequency B-Spline wavelet |
|
Gaussian wavelet |
|
Mexican hat wavelet |
|
Meyer wavelet |
|
Meyer wavelet auxiliary function |
|
Morlet wavelet |
|
Reverse biorthogonal spline wavelet filters |
|
Complex Shannon wavelet |
|
Symlet wavelet filter computation |
|
Symlet wavelet filter |
Continuous Wavelet: One-Dimensional
|
Continuous 1-D wavelet coefficients |
|
Build a wavelet starting from a pattern |
Discrete Wavelets: One-Dimensional
|
1-D approximation coefficients |
|
1-D detail coefficients |
|
Single-level discrete 1-D wavelet transform |
|
Discrete wavelet transform extension mode |
|
Single-level inverse discrete 1-D wavelet transform |
|
Direct reconstruction from 1-D wavelet coefficients |
|
Single-level reconstruction of 1-D wavelet decomposition |
|
Multilevel 1-D wavelet decomposition |
|
Multilevel 1-D wavelet reconstruction |
|
Energy for1-D wavelet decomposition |
|
Reconstruct single branch from 1-D wavelet coefficients |
Discrete Wavelets: Two-Dimensional
|
2-D approximation coefficients |
|
2-D detail coefficients |
|
Single-level discrete 2-D wavelet transform |
|
Discrete wavelet transform extension mode |
|
Single-level inverse discrete 2-D wavelet transform |
|
Direct reconstruction from 2-D wavelet coefficients |
|
Single-level reconstruction of 2-D wavelet decomposition |
|
Multilevel 2-D wavelet decomposition |
|
Multilevel 2-D wavelet reconstruction |
|
Energy for 2-D wavelet decomposition |
|
Reconstruct single branch from 2-D wavelet coefficients |
Wavelet Packet Algorithms
|
Best level tree wavelet packet analysis |
|
Best tree wavelet packet analysis |
|
Entropy update (wavelet packet) |
|
Energy for wavelet packet decomposition |
|
Entropy (wavelet packet) |
|
Extract wavelet tree from wavelet packet tree |
|
Wavelet packet coefficients |
|
Cut wavelet packet tree |
|
Wavelet packet decomposition 1-D |
|
Wavelet packet decomposition 2-D |
|
Wavelet packet functions |
|
Recompose wavelet packet |
|
Reconstruct wavelet packet coefficients |
|
Wavelet packet reconstruction 1-D |
|
Wavelet packet reconstruction 2-D |
|
Split (decompose) wavelet packet |
Discrete Stationary Wavelet Transform Algorithms
|
Inverse discrete stationary wavelet transform 1-D |
|
Inverse discrete stationary wavelet transform 2-D |
|
Discrete stationary wavelet transform 1-D |
|
Discrete stationary wavelet transform 2-D |
Lifting Wavelet Transform for Signals/Images
|
Add lifting steps to lifting scheme |
|
Biorthogonal scaling and wavelet functions |
|
Display lifting scheme |
|
Transform quadruplet of filters to lifting scheme |
|
Inverse 1-D lifting wavelet transform |
|
Inverse 2-D lifting wavelet transform |
|
Apply elementary lifting steps on quadruplet of filters |
|
Lifting schemes |
|
Laurent matrices constructor |
|
Laurent polynomials constructor |
|
Transform lifting scheme to quadruplet of filters |
|
Lifting schemes information |
|
1-D lifting wavelet transform |
|
2-D lifting wavelet transform |
|
Extract or reconstruct 1-D LWT wavelet coefficients |
|
Extract or reconstruct 2-D LWT wavelet coefficients |
|
Laurent polynomials associated with wavelet |
|
Wavelet names for LWT |
De-Noising and Compression for Signals/Images
|
Default values for de-noising or compression |
|
Threshold selection for de-noising |
|
Penalized threshold for wavelet 1-D or 2-D de-noising |
|
Thresholds for wavelet 1-D using Birge-Massart strategy |
|
Thresholds for wavelet 2-D using Birge-Massart strategy |
|
Automatic 1-D de-noising |
|
De-noising or compression |
|
Noisy wavelet test data |
|
Estimate noise of 1-D wavelet coefficients |
|
Penalized threshold for wavelet packet de-noising |
|
De-noising or compression using wavelet packets |
|
Wavelet packet coefficients thresholding |
|
Wavelet coefficient thresholding 1-D |
|
Wavelet coefficient thresholding 2-D |
|
Soft or hard thresholding |
|
Threshold settings manager |
Other Wavelet Applications
|
Fractional Brownian motion synthesis |
|
Parameter estimation of fractional Brownian motion |
|
Fusion of two images |
|
Fusion of two matrices or arrays |
Tree Management Utilities
|
Tree nodes |
|
Wavelet packet tree construction from coefficients |
|
Node depth-position to node index |
|
WPTREE information |
|
Draw wavelet packet decomposition tree (GUI) |
|
Data trees (DTREE) constructor |
|
Get tree (WPTREE) contents |
|
Node index to node depth-position |
|
Existing node test |
|
Terminal nodes indices test |
|
Determine terminal nodes |
|
Node ascendants |
|
Node descendants |
|
Recompose node |
|
Node parent |
|
Split (decompose) node |
|
Determine nonterminal nodes |
|
Number of terminal nodes |
|
NTREE constructor |
|
Plot tree object |
|
Read values of WPTREE |
|
Read wavelet packet decomposition tree from a figure |
|
Set WPTREE field contents |
|
Determine terminal nodes |
|
Tree depth |
|
Tree order |
|
Constructor for the class WPTREE |
|
Plot wavelet packets colored coefficients |
|
Write values in WPTREE fields |
|
WTBO constructor |
|
NTREE manager |
General Utilities
|
Extended pseudocolor matrix scaling |
|
Extend vector or matrix |
|
Keep part of vector or matrix |
|
Flip vector |
|
Wavelet Toolbox manager |
Miscellaneous Functions and Demos
|
Find variance change points |
|
Wavelet information |
|
Wavelet toolbox demos |
 | Function Reference | Functions -- Alphabetical List |  |
© 1994-2005 The MathWorks, Inc.